Badanie przecięcia promień-sfera
1
2
3
4
5
6
7
8
9
10
11
| inline float intersect(sphere::i S, ray::i r) {
vec3 v = r.origin - S.center;
float b = dotProd(v, r.aheadDir);
float d2 = b*b - dotProd(v,v) + S.radius*S.radius;
if (d2 < 0.0f) return undefined;
float d = sqrt(d2);
float t1 = -b-d, t2 = -b+d;
if (t1 > epsilon5) return t1;
if (t2 > epsilon5) return t2;
return undefined;
} |
Równanie sfery:
Wstawiając
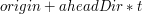
za
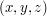
otrzymujemy równanie:
Równanie to można zapisać (grupując wyrazy ze względu na

) jako:
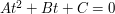
, gdzie:
Jeśli 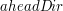 ma długość
ma długość  (a dbamy o to, żeby tak było), to
(a dbamy o to, żeby tak było), to 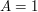 .
Przyspiesza to nieco obliczenia, a pierwiaski równania
.
Przyspiesza to nieco obliczenia, a pierwiaski równania 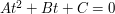 możemy obliczyć ze wzorów:
możemy obliczyć ze wzorów:
W wierszach nr 2-4 obliczamy
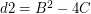
.
W wierszu nr 5 sprawdzamy czy
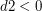
, jeśli tak jest, to równanie
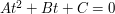
nie ma rozwiązań.
W przeciwnym wypadku przechodzimy do wierszy nr 6-7 i obliczamy
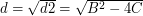
,
a nastepnie
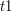
i
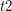
.
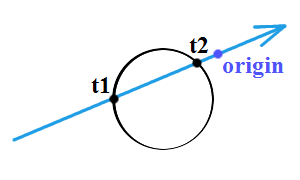
Szukamy najbliższego przecięcia, a więc interesuje nas ta wartość  , która jest większa od zera
(jeśli
, która jest większa od zera
(jeśli  jest mniejsza od zera, to punkt przecięcia jest za źródłem, a nie przed źródłem promienia
względem kierunku ruchu).
Istnieją teraz trzy możliwe sytuacje rozpatrywane w wierszach 8-10.
jest mniejsza od zera, to punkt przecięcia jest za źródłem, a nie przed źródłem promienia
względem kierunku ruchu).
Istnieją teraz trzy możliwe sytuacje rozpatrywane w wierszach 8-10.
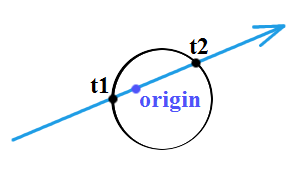
1) 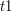 oraz
oraz 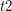 są większe od zera, a bliższe przecięcie opisuje
są większe od zera, a bliższe przecięcie opisuje 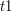 .
.
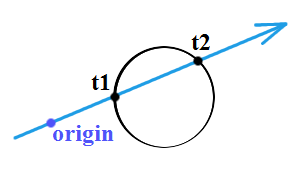
2) Tylko 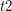 jest większe od zera, a więc opisuje interesujące nas przecięcie
jest większe od zera, a więc opisuje interesujące nas przecięcie 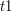 .
.
3) 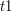 oraz
oraz 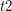 są mniejsza od zera, a więc brak przecięć.
są mniejsza od zera, a więc brak przecięć.
Badanie przecięcia promień-trójkąt
Do badania przecięcia promienia z trójkątem będziemy potrzebowali
funkcji obliczającej pole trójkąta reprezentowanego przez trzy punkty.
Uzyjemy do tego implementacji wzoru Herona.
1
2
3
4
5
6
7
| inline float area(vec3::i v1, vec3::i v2, vec3::i v3) {
float a = length(v2 - v1);
float b = length(v3 - v1);
float c = length(v3 - v2);
float p = (a + b + c) / 2.0f;
return sqrt(p*(p-a)*(p-b)*(p-c));
} |
Badanie przecięcia odbywa się w dwóch etapach.
Pierwszy etap polega na znalezieniu punktu przecięcia promienia
z płaszczyzną, na której leży trójkąt.
Przypomnijmy, że
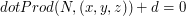 to równanie płaszczyzny trójkąta
to równanie płaszczyzny trójkąta
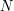 to wektor normalny do powierzchni trójkąta
to wektor normalny do powierzchni trójkąta
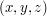 to dowolny punkt przestrzeni
to dowolny punkt przestrzeni
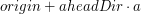 oznacza punkty na prostej po której podróżuje promień
oznacza punkty na prostej po której podróżuje promień
Podstawiamy 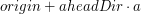 za
za 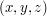 otrzymując równanie
otrzymując równanie
które rozwiązujemy ze względu na

.
Z rozwiązania otrzymujemy, że
Jeśli

jest większe od zera oraz nie jest nieskończonością, to nasz promień trafia w płaszczyznę,
na której leży trójkąt. Poniżej kod procedury badającej przecięcia,
etap pierwszy wykonywany jest w wierszach 2-5 procedury
.
1
2
3
4
5
6
7
8
9
10
11
12
13
| inline float intersect(triangle::i T, ray::i r) {
float t = (-T.d - dotProd(T.N, r.origin)) / dotProd(T.N, r.aheadDir);
if ( !(t > epsilon5 && t < infinity) )
return undefined;
vec3 ip = r.origin + r.aheadDir * t;
float abc = area(T.v1 , T.v2 , T.v3);
float pbc = area( ip , T.v2 , T.v3);
float apc = area(T.v1 , ip , T.v3);
float abp = area(T.v1 , T.v2 , ip );
if ( pbc + apc + abp > abc + epsilon3 )
return undefined;
return t;
} |
Mając punkt przecięcia promienia z płaszczyzną trójkąta (jest to punkt 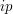 obliczony w wierszu nr 5)
możemy przystąpić do drugiego etapu badania przeciącia promienia z trójkętem. Drugi etap polega
na sprawdzeniu czy punkt przecięcia promienia z płaszczyzną leży wewnątrz trójkąta.
obliczony w wierszu nr 5)
możemy przystąpić do drugiego etapu badania przeciącia promienia z trójkętem. Drugi etap polega
na sprawdzeniu czy punkt przecięcia promienia z płaszczyzną leży wewnątrz trójkąta.
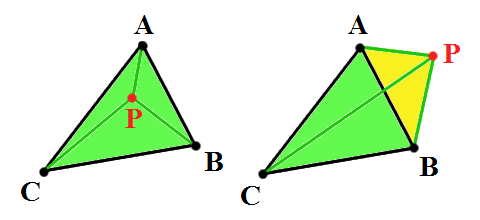
Niech  ,
,  ,
,  oznaczają wierzchołki
oznaczają wierzchołki 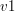 ,
, 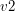 ,
, 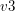 naszego trójkąta, a
naszego trójkąta, a  oznacza punkt przecięcia
oznacza punkt przecięcia 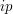 .
Aby sprawdzić czy
.
Aby sprawdzić czy 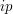 leży wewnątrz trójkąta należy sprawdzić czy suma pól trójkątów
leży wewnątrz trójkąta należy sprawdzić czy suma pól trójkątów 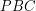 ,
, 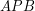 ,
, 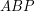 jest równa polu trójkąta
jest równa polu trójkąta 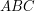 (wtedy punkt
(wtedy punkt 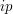 leży wewnątrz trójkąta), czy jest większa od pola trójkąta
leży wewnątrz trójkąta), czy jest większa od pola trójkąta 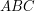 (wtedy punkt
(wtedy punkt 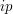 leży poza trójkątem). Tutaj też jednak narażeni jesteśmy na pułapkę.
Z powodu niedokładnej reprezentacji liczb rzeczywistych nie jesteśmy w stanie sprawdzać równości wyżej
wymienionych pól trójkątów, więc sprawdzamy czy suma pól trójkątów
leży poza trójkątem). Tutaj też jednak narażeni jesteśmy na pułapkę.
Z powodu niedokładnej reprezentacji liczb rzeczywistych nie jesteśmy w stanie sprawdzać równości wyżej
wymienionych pól trójkątów, więc sprawdzamy czy suma pól trójkątów 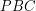 ,
, 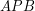 oraz
oraz 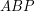 jest większa
od pola trójkąta
jest większa
od pola trójkąta 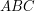 zwiększonego o pewną małą wartość.
Etap drugi wykonywany jest w wierszach 6-12 procedury
zwiększonego o pewną małą wartość.
Etap drugi wykonywany jest w wierszach 6-12 procedury 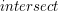 .
.
Błędy numeryczne
Gdy promień trafi w pewien punkt 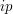 , a następnie wygenerujemy np. promień odbity,
to źródłem tego promienia będzie właśnie punkt
, a następnie wygenerujemy np. promień odbity,
to źródłem tego promienia będzie właśnie punkt 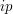 . Procedura dokonująca śledzenia promienia
dokona testu przecięcia również z obiektem, od którego ten promień się odbija.
W czym problem? Odległość punktu
. Procedura dokonująca śledzenia promienia
dokona testu przecięcia również z obiektem, od którego ten promień się odbija.
W czym problem? Odległość punktu 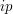 od nowego punktu przecięcia powinna wynosić zero,
niestety z powodu niedokładnej reprezentacji liczb rzeczywistych w komputerze
na ogół tak nie będzie. Będzie to wartość bardzo bliska zeru, ale jednak nie zero.
Procedura śledząca promień uzna więc, że obiekt, od którego promień się odbija jest
najbliższym obiektem przecinającym nasz odbity promień, co oczywiście jest błędem,
który prowadzi do sytuacji, w której z obliczeń wynika, że powierzchnia sama sobie
zasłania źródło światła mimo, że jest to nieprawdą. Skutkuje to błędnym niedoświetleniem różnych punktów sceny
objawiajacego się ziarnistym szumem. Oto efekt omawianych błędów obliczeniowych:
od nowego punktu przecięcia powinna wynosić zero,
niestety z powodu niedokładnej reprezentacji liczb rzeczywistych w komputerze
na ogół tak nie będzie. Będzie to wartość bardzo bliska zeru, ale jednak nie zero.
Procedura śledząca promień uzna więc, że obiekt, od którego promień się odbija jest
najbliższym obiektem przecinającym nasz odbity promień, co oczywiście jest błędem,
który prowadzi do sytuacji, w której z obliczeń wynika, że powierzchnia sama sobie
zasłania źródło światła mimo, że jest to nieprawdą. Skutkuje to błędnym niedoświetleniem różnych punktów sceny
objawiajacego się ziarnistym szumem. Oto efekt omawianych błędów obliczeniowych:

Jak sobie z tym poradzić?
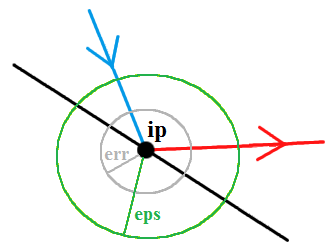
Śledzony promień (niebieski) trafił w punkt 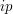 , po czym wygenerowaliśmy promień odbity (czerwony)
i rozpoczynamy dla niego procedurę śledzenia. Jeśli w wyniku śledzenia promienia odbitego otrzymamy
nowy punkt przecięcia, który znajduje się w obszarze o promieniu
, po czym wygenerowaliśmy promień odbity (czerwony)
i rozpoczynamy dla niego procedurę śledzenia. Jeśli w wyniku śledzenia promienia odbitego otrzymamy
nowy punkt przecięcia, który znajduje się w obszarze o promieniu 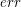 (rozmiar błędu wynikającego z niedokładnej reprezentacji liczb rzeczywistych) na powyższej ilustracji,
to najpewniej jest to wynik błędów numerycznych. Stąd akceptujemy tylko punkty leżące poza obszarem
o promieniu
(rozmiar błędu wynikającego z niedokładnej reprezentacji liczb rzeczywistych) na powyższej ilustracji,
to najpewniej jest to wynik błędów numerycznych. Stąd akceptujemy tylko punkty leżące poza obszarem
o promieniu 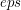 odrzucając wszystkie błędne punkty przecięcia stwarzając jednak możliwość
odrzucenia potencjalnie dobrych punktów. Dobieramy jednak wartość
odrzucając wszystkie błędne punkty przecięcia stwarzając jednak możliwość
odrzucenia potencjalnie dobrych punktów. Dobieramy jednak wartość 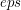 jako liczbę bardzo małą,
np.
jako liczbę bardzo małą,
np. 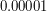 minimalizując szansę na odrzucenie poprawnego punktu przeciącia.
minimalizując szansę na odrzucenie poprawnego punktu przeciącia.




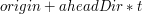 za
za 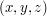 otrzymujemy równanie:
otrzymujemy równanie:
 ) jako:
) jako: 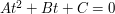 , gdzie:
, gdzie:
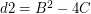 .
. 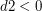 , jeśli tak jest, to równanie
, jeśli tak jest, to równanie 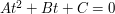 nie ma rozwiązań.
W przeciwnym wypadku przechodzimy do wierszy nr 6-7 i obliczamy
nie ma rozwiązań.
W przeciwnym wypadku przechodzimy do wierszy nr 6-7 i obliczamy 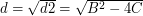 ,
a nastepnie
,
a nastepnie 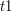 i
i 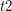 .
.



 .
Z rozwiązania otrzymujemy, że
.
Z rozwiązania otrzymujemy, że
 jest większe od zera oraz nie jest nieskończonością, to nasz promień trafia w płaszczyznę,
na której leży trójkąt. Poniżej kod procedury badającej przecięcia,
etap pierwszy wykonywany jest w wierszach 2-5 procedury
jest większe od zera oraz nie jest nieskończonością, to nasz promień trafia w płaszczyznę,
na której leży trójkąt. Poniżej kod procedury badającej przecięcia,
etap pierwszy wykonywany jest w wierszach 2-5 procedury 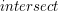 .
.





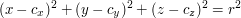
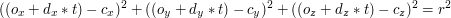
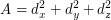
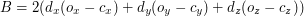
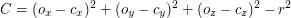
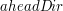 ma długość
ma długość  (a dbamy o to, żeby tak było), to
(a dbamy o to, żeby tak było), to 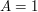 .
Przyspiesza to nieco obliczenia, a pierwiaski równania
.
Przyspiesza to nieco obliczenia, a pierwiaski równania 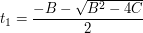
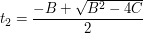
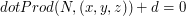 to równanie płaszczyzny trójkąta
to równanie płaszczyzny trójkąta 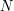 to wektor normalny do powierzchni trójkąta
to wektor normalny do powierzchni trójkąta 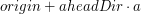 oznacza punkty na prostej po której podróżuje promień
oznacza punkty na prostej po której podróżuje promień
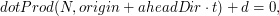
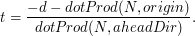
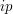 obliczony w wierszu nr 5)
możemy przystąpić do drugiego etapu badania przeciącia promienia z trójkętem. Drugi etap polega
na sprawdzeniu czy punkt przecięcia promienia z płaszczyzną leży wewnątrz trójkąta.
obliczony w wierszu nr 5)
możemy przystąpić do drugiego etapu badania przeciącia promienia z trójkętem. Drugi etap polega
na sprawdzeniu czy punkt przecięcia promienia z płaszczyzną leży wewnątrz trójkąta.
 ,
,  ,
,  oznaczają wierzchołki
oznaczają wierzchołki 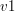 ,
, 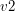 ,
, 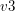 naszego trójkąta, a
naszego trójkąta, a  oznacza punkt przecięcia
oznacza punkt przecięcia 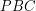 ,
, 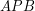 ,
, 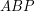 jest równa polu trójkąta
jest równa polu trójkąta 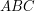 (wtedy punkt
(wtedy punkt 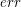 (rozmiar błędu wynikającego z niedokładnej reprezentacji liczb rzeczywistych) na powyższej ilustracji,
to najpewniej jest to wynik błędów numerycznych. Stąd akceptujemy tylko punkty leżące poza obszarem
o promieniu
(rozmiar błędu wynikającego z niedokładnej reprezentacji liczb rzeczywistych) na powyższej ilustracji,
to najpewniej jest to wynik błędów numerycznych. Stąd akceptujemy tylko punkty leżące poza obszarem
o promieniu 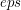 odrzucając wszystkie błędne punkty przecięcia stwarzając jednak możliwość
odrzucenia potencjalnie dobrych punktów. Dobieramy jednak wartość
odrzucając wszystkie błędne punkty przecięcia stwarzając jednak możliwość
odrzucenia potencjalnie dobrych punktów. Dobieramy jednak wartość 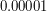 minimalizując szansę na odrzucenie poprawnego punktu przeciącia.
minimalizując szansę na odrzucenie poprawnego punktu przeciącia.


