Wyszukiwanie binarne
26.11.2009 - Marcin Oczeretko
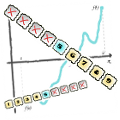
 W jaki sposób szybko znajdować wartości w posortowanym zbiorze? Istnieje sprytny sposób na sprawne rozwiązywanie tego problemu - wyszukiwanie binarne. Poniższy artykuł umożliwi Wam zapoznanie się z tym potężnym i zarazem bardzo prostym algorytmem. Wyszukiwanie binarne pozwala na sprawne odszukiwanie wartości w posortowanych zbiorach. Jest to jednocześnie chyba jeden z najbardziej intuicyjnych algorytmów. Ludzie dość często korzystają ze zbliżonych do niego sposobów i zwykle nawet nie zdają sobie z tego sprawy. Czasami próbując odnaleźć swoje nazwisko czy też pesel na posegregowanej liście, staramy się "wstrzelić" w odpowiedni jej fragment, oszacować jakoś pozycję interesującego nas wpisu. Jest to strategia niezwykle podobna do tej, którą posługujemy się przy wyszukiwaniu binarnym. Aby wytworzyć pewną intiucję, przydatną przy dalszych rozważaniach, proponuję byście zagrali kilka razy w umieszczoną poniżej "grę". Wasz oponent wybiera na początku liczbę całkowitą z zakresu od
Dodatkowo dzięki tej taktyce jesteśmy odporni na nieuczciwych przeciwników! Nawet jeśli oponent będzie tak dobierał odpowiedzi na nasze pytania, byśmy musieli zadawać ich jak najwięcej, możemy zakończyć grę po najwyżej pięciu strzałach. Zauważ, że gdybyśmy wymieniali liczby po kolei ( Wszystkie powyższe obserwacje sprawiają, że jesteśmy już tylko o krok od algorytmu wyszukiwania binarnego.
(13 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


 do
do 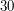 , a Wy staracie się ją odgadnąć, zadając jak najmniejszą ilość zapytań. Możecie jedynie sprawdzać, czy wytypowana przez Was liczba jest mniejsza, równa bądź większa, niż ta wybrana przez przeciwnika.
, a Wy staracie się ją odgadnąć, zadając jak najmniejszą ilość zapytań. Możecie jedynie sprawdzać, czy wytypowana przez Was liczba jest mniejsza, równa bądź większa, niż ta wybrana przez przeciwnika.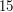 , liczby od
, liczby od 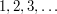 ), to ilość pytań może wynieść nawet
), to ilość pytań może wynieść nawet 

