Pierwsza większa:
Zmodyfikuj nieco algorytm wyszukiwania binarnego tak, by znajdować w posortowanym niemalejąco ciągu pierwszą liczbę większą niż podana wartość.
Wejście:
Pierwszy wiersz zawiera dwie liczby naturalne  i
i  (
(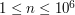 ,
, 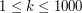 ).
).
W drugiej linijce pojawi się  liczb:
liczb: 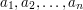 (
(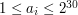 ).
).
W trzeciej linijce będzie  liczb:
liczb: 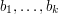 (
(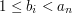 )
)
Wyjście:
Dla każdej liczby 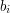 z trzeciego wiersza należy wypisać w osobnym wierszu taką liczbę
z trzeciego wiersza należy wypisać w osobnym wierszu taką liczbę 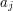 spośród
spośród 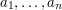 , że zachodzi nierówność:
, że zachodzi nierówność:
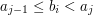
Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany.
Zaloguj się lub
załóż konto.
Słownik:
Przeszukiwać binarnie możemy nie tylko ciągi zawierające same liczby. Algorytm ten poradzi sobie z każdym posortowanym zbiorem! Aby się o tym przekonać, napisz program, który sprawdzi czy podany wyraz występuje na uporządkowanej alfabetycznie liście różnych słów. Jeśli tak będzie to wypisuj jego pozycję.
Wejście:
W pierwszym wierszu podana zostanie liczba naturalna  (
(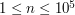 ).
).
W  kolejnych wierszach dostaniesz
kolejnych wierszach dostaniesz  uporządkowanych alfabetycznie słów:
uporządkowanych alfabetycznie słów: 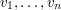 .
.
Kolejny wiersz zawierać będzie liczbę naturalną  (
(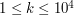 ).
).
W  kolejnych wierszach podanych zostanie
kolejnych wierszach podanych zostanie  słów:
słów: 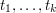 .
.
Możesz założyć, że wszystkie słowa na wejściu będą miały taką samą długość, która nie przekroczy 10 znaków.
Wyjście:
Powinno składać się z i wierszy. W i-tym wierszu należy:
- jeśli
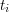 występuje wśród wyrazów
występuje wśród wyrazów 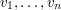 : wypisać pozycję, na której możemy to słowo odnaleźć,
: wypisać pozycję, na której możemy to słowo odnaleźć,
- w przeciwnym wypadku: wypisać "NIE".
Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany.
Zaloguj się lub
załóż konto.
Miejsce zerowe
Przećwiczmy jeszcze wyszukiwanie miejsc zerowych funkcji. Napisz program, który dla danego wielomianu piątego stopnia w(x) poda jego miejsce zerowe w zaokrągleniu do 10 cyfr po przecinku. Dane wejściowe będą tak dobrane, by istniała tylko jedna taka wartość 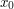 , że
, że 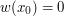 . Prawdziwa też będzie nastepująca nierówność:
. Prawdziwa też będzie nastepująca nierówność:
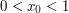
Wejście:
Wejście składa się z jednej linii, zawierającej 6 liczb rzeczywistych: 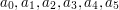
Wyjście:
Wypisz miejsce zerowe wielomianu 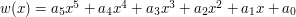 w zaokrągleniu do 10 cyfr po przecinku. Należy wypisać dokładnie 10 cyfr z rozwinięcia dziesiętnego liczby (np. jeśli w zmiennej wynik typu double mamy wyliczone poprawnie 11 pierwszych cyfr po przecinku, to w języku C wypisujemy prawidłową wartość za pomocą printf("%.10lf",wynik) ).
w zaokrągleniu do 10 cyfr po przecinku. Należy wypisać dokładnie 10 cyfr z rozwinięcia dziesiętnego liczby (np. jeśli w zmiennej wynik typu double mamy wyliczone poprawnie 11 pierwszych cyfr po przecinku, to w języku C wypisujemy prawidłową wartość za pomocą printf("%.10lf",wynik) ).
Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany.
Zaloguj się lub
załóż konto.



 i
i  (
(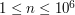 ,
, 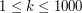 ).
).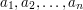 (
(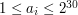 ).
).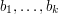 (
(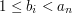 )
) 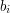 z trzeciego wiersza należy wypisać w osobnym wierszu taką liczbę
z trzeciego wiersza należy wypisać w osobnym wierszu taką liczbę 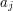 spośród
spośród 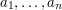 , że zachodzi nierówność:
, że zachodzi nierówność: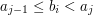
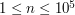 ).
).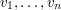 .
.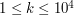 ).
).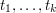 .
.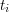 występuje wśród wyrazów
występuje wśród wyrazów 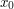 , że
, że 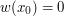 . Prawdziwa też będzie nastepująca nierówność:
. Prawdziwa też będzie nastepująca nierówność: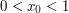
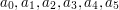
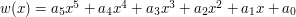 w zaokrągleniu do 10 cyfr po przecinku. Należy wypisać dokładnie 10 cyfr z rozwinięcia dziesiętnego liczby (np. jeśli w zmiennej wynik typu double mamy wyliczone poprawnie 11 pierwszych cyfr po przecinku, to w języku C wypisujemy prawidłową wartość za pomocą printf("%.10lf",wynik) ).
w zaokrągleniu do 10 cyfr po przecinku. Należy wypisać dokładnie 10 cyfr z rozwinięcia dziesiętnego liczby (np. jeśli w zmiennej wynik typu double mamy wyliczone poprawnie 11 pierwszych cyfr po przecinku, to w języku C wypisujemy prawidłową wartość za pomocą printf("%.10lf",wynik) ).

