 Pisząc ten artykuł postanowiłem, że nie zdradzę ani jednego rozwiązania, bo odebrałbym Wam dużo radości.
Nie mam ulubionego zadania, ani nie umiem opowiedzieć poruszającej historii na temat zawodów, mogę jednak podzielić się próbką problemów, których rozwiązania na zawsze utkwiły mi w głowie. Oto one, wraz z delikatnymi podpowiedziami.
Pisząc ten artykuł postanowiłem, że nie zdradzę ani jednego rozwiązania, bo odebrałbym Wam dużo radości.
Nie mam ulubionego zadania, ani nie umiem opowiedzieć poruszającej historii na temat zawodów, mogę jednak podzielić się próbką problemów, których rozwiązania na zawsze utkwiły mi w głowie. Oto one, wraz z delikatnymi podpowiedziami.
Dany jest zbiór niedużych nominałów funkcjonujących w obiegu, oraz kwota x. Czy x da się w ogóle wypłacić używając podanych nominałów?
To zadanie uświadomiło mi, że nawet w algebrze można dopatrzeć się teorii grafów.
Małpki wiszą trzymając się łapkami drzewa bądź innych małp, ale każda małpka po pewnym czasie nie wytrzymuje i puszcza łapki. Należy dla każdej małpki powiedzieć kiedy zleci z drzewa.
To zadanie było pierwszym, które uświadomiło mi, że odwracanie ogona kotem, to jedno z podstawowych narzędzi w pracy intelektualnej informatyka.
Metodologia przydatna do zadań takich jak Island, problem optymalnego zarządzania pamięcią podręczną offline, czy też w innym olimpijskim zadaniu: dla zadanego grafu policz ile jest takich trójek wierzchołków, że są kliką bądź zbiorem niezależnym.
Na lodowisku oprócz prostokątnej bandy znajdują się równoległe i prostopadłe barierki. Jako łyżwiarz mogący przesuwać się wzdłuż poręczy, bądź odpychać się od niej prostopadle i sunąć jednostajnie po tafli, chcesz dotrzeć z A do B.
To zadanie pomimo legendarnej trudności, okazało się całkiem proste do zaimplementowania i tym samym uświadomiło mi, że nie wolno się poddawać. Gdyby nie to, nie zabierałbym się za Świątynie ani Chmury z PA
O zadaniu pisał Marcin Bieńkowski, ale nie napisał chyba, że problem sprawdzenia czy jedno słowo jest cyklicznym przesunięciem drugiego można rozwiązać w stałej dodatkowej pamięci.
Wtedy na PA, wysłałem chyba rozwiązanie używające strstr na ciągach intów zxorowanych z 0x01010100.
Rozwiązanie ze stałą dodatkową pamięcią poznałem później i okazało się rozwiązywać też problem maksymalnego sufiksu, potrzebny w transformacie Burrowsa-Wheelera, oraz wyszukiwać dowolny wzorzec w tekście w stałej dodatkowej pamięci -- coś co do dziś uważam za niesamowity kawałek informatyki.
Na stronie IBM jest pełno zagadek, a w śród nich znalazłem kiedyś taką zagadkę: wśród n+1 liczb naturalnych z zakresu 1..n, znajdź jakąś, która się powtarza używając stałej dodatkowej pamięci.
Zadanie ma wiele fajnych wersji z zupełnie różnymi rozwiązaniami. W jednej z nich jest tylko jeden duplikat co pozwala problem rozwiązać arytmetycznie. Natomiast ten oryginalny pojawia się na przesłuchaniach do Microsoftu, tyle, że w wersji o walidacji list jednokierunkowych.
Na rozmowie do Google dostałem wersję: znajdź pierwszy od lewej zduplikowany element. W stresie wymyśliłem tylko algorytm 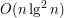 .
.
 3-SAT
3-SAT
Dla zadanej formuły w postaci 3-CNF określ ile procent wartościowań ją spełnia z dokładnością do 1%.
To jedno z takich zadań, którego rozwiązanie ma się ochotę potem dopasowywać na siłę do innych problemów. Na przykład ja chciałem w ten sam sposób rozwiązać problem części wspólnej 3 kul, który pojawił się na CEPC 2009.
Muszę się przyznać, że na PA rozwiązałem to zadanie zupełnie inaczej: napisałem prosty dekompresor oraz sat-solver i zamiast stablicować wyniki, mój program rozwiązywał zadanie na żywo -- niepotrzebne do niczego ryzyko, ale ile radości.
Znając ilościowe rezerwacje złożone przez pasażerów pociągu, czyli trójki (skąd,dokąd,ile_osób) sprawdź czy da się je zrealizować.
Zaproponuj system informujący on-line pozwalający dodawać i anulować takie rezerwacje.
To zadanie było pierwszym, przy którym wiele osób z "mojego pokolenia" zetknęło się ze strukturą danych nazywaną odtąd przez nas "koleje", co w sumie nieźle pasowało do jej wagonikowatego wyglądu. Wersja offline jest znacznie prostsza i odtąd idiomy typu events.push_back(make_pair(START,from)) zagościły w moich rozwiązaniach niejednego problemu z zamiataniem.
W skierowanym grafie odwiedzenie niektórych wierzchołków kosztuje -- czy istnieje droga z A do B o koszcie dokładnie X?
Oczywiście dodatkowy wymóg, że droga ma nie zawierać samoprzecięć znacząco utrudniłby nam życie. Podobnież, gdyby X mogło być duże. Na szczęście oryginalna wersja tego zadania ma bardzo ładne rozwiązanie dynamiczne, które paru moich znajomych nazywa na cześć tego zadania "zamkiem".
 Łańcuch mocy kontinuum w
Łańcuch mocy kontinuum w 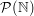
Nie samymi konkursami człowiek żyje i niektóre zadania poszerzają horyzonty choć pojawiły się na studiach a nie na zawodach -- jeśli ktoś nie wierzy, to zapraszam na Logikę dla Informatyków na UWr.
W tym zadaniu należy wskazać rodzinę podzbiorów zbioru liczb naturalnych taką, że dla każdych dwóch jej elementów jeden zawiera się w drugim bądź na odwrót, która ma więcej elementów niż jest liczb naturalnych. Przy okazji warto się zastanowić czy istnieje antyłańcuch. Nie wiem dlaczego zawsze przy takich dualizmach przypomina mi się zadanie: pokaż, że każdy ciąg n liczb zawiera podciąg monotoniczny o 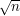 elementach, oraz drugie, że każdy DAG zawiera łańcuch bądź antyłańcuch takiej długości.
elementach, oraz drugie, że każdy DAG zawiera łańcuch bądź antyłańcuch takiej długości.
Za to zadanie dostałem kiedyś przy tablicy grzyba, bo próbowałem przepchnąć dowód, że taka rodzina nie istnieje, co jest dość logiczną konsekwencją faktu, że jak weźmiemy dwa kolejne elementy łańcucha, to przecież możemy wbić pinezkę w najmniejszą liczbę, którą się różnią. To zadanie (jak parę innych) nauczyło mnie odtąd bardzo skrupulatnie przyglądać się moim własnym rozumowaniom, a w szczególności nie zakładać tezy już na starcie.
 Pierwiastek modulo
Pierwiastek modulo
Kolejne zadanie pochodzi z Matematyki Dyskretnej, Kombinatoryki bądź Kryptografii, których to przedmiotów z perspektywy czasu nie rozróżniam. Dla zadanego y i n, należy znaleźć takie x, że 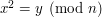 . Dla uproszczenia można przyjąć, że n jest liczbą pierwszą.
. Dla uproszczenia można przyjąć, że n jest liczbą pierwszą.
Co ciekawe trudność problemu znacząco się różni w zależności od reszty z dzielenia n przez 4.
Jest to jedno z takich zadań, które średnio raz na rok muszę sobie z powrotem przypominać jak się robiło i za każdym razem jestem dumny, że znów dałem radę.
 Układ równań na liczbach całkowitych
Układ równań na liczbach całkowitych
Dla zadanej macierzy liczb całkowitych  oraz wektora liczb całkowitych
oraz wektora liczb całkowitych 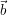 , znajdź taki wektor liczb całkowitych
, znajdź taki wektor liczb całkowitych 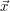 , że
, że 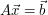 .
.
Podobnie jak większość ludzi, byłem przekonany, że wersja dla liczb wymiernych jest wielomianowa -- owszem to prawda, ale dojście do niej zajęło nam kilka wykładów i ćwiczeń. Podobnie jak większość ludzi, myślałem, że powyższa wersja jest NP-trudna, poprzez łudzące podobieństwo do wersji z liczbami naturalnymi -- ku mojemu zaskoczeniu istnieje jednak algorytm wielomianowy.
Za oba odkrycia dziękuję doktorowi Antoniemu Kościelskiemu i Równaniom i Nierównościom Liniowym.
Dla zadanego zbioru wielokątów wyznacz maksymalną możliwą liczbę przecięć prostej z ich obrysami.
Choć zadanie ma pewnie sporo rozwiązań, ja
najbardziej cieszę się z tego, że na Geometrii Obliczeniowej nauczyłem się iż Dual Plane, to ani nie dwupłatowiec, ani nie frame buffer w OpenGL, tylko kolejny ogon, za który można wywijać kotami.
Nazwy zadań powyżej są klikalnymi linkami do oryginalnych treści



