Pająki
13.11.2009 - Marcin Bieńkowski
  Dłuższą chwilę zastanawiałem się jak nie zacząć tekstu od frazy ,,moim ulubionym zadaniem''. Poszło łatwiej niż sądziłem, gdyż Pająki (o których jest ten artykuł), są jednym z zadań, które dostarczyły mi głównie mnóstwo frustracji, choć również jeszcze więcej satysfakcji z oszukania systemu. Opisane w tym artykule rozwiązanie zadania wydaje się ciekawe, gdyż redukuje problem grafowy do problemu wyszukiwania wzorca (a nie — jak to zwykle bywa — na odwrót). Ale zacznijmy od początku. Pełną treść owego zadania z Pogromców Algorytmów (to takie Potyczki Algorytmiczne dla tetryków) można znaleźć na przykład tutaj. W telegraficznym skrócie: mamy dwa grafy i musimy stwierdzić, czy są one izomorficzne. Oznacza to sprawdzenie, czy da się tak ponumerować wierzchołki każdego z nich, żeby para wierzchołków o numerach a i b była połączona w pierwszym grafie dokładnie wtedy, jeśli jest połączona w drugim grafie.
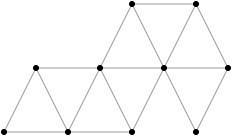
IzomorfizmJak powszechnie wiadomo, dokładnie nie wiadomo jaka jest złożoność problemu sprawdzania, czy dwa grafy są izomorficzne. Dla naszych celów wystarczy, że nieznany jest algorytm wielomianowy. Dla grafów planarnych (a takie są grafy opisane w zadaniu), sytuacja jest trochę lepsza: istnieją algorytmy i to nawet działające w czasie liniowym. Jednak wrodzone lenistwo powstrzymało mnie przed skomplikowaną implementacją takiego algorytmu. Trywialnym warunkiem koniecznym izomorfizmu jest równa liczba wierzchołków w obu grafach; od tej chwili będziemy zakładać że warunek taki zachodzi a liczbę tę oznaczać przez n. Przyjrzyjmy się dokładniej temu, jak tworzone są grafy. Dla łatwiejszej wizualizacji umieśćmy ich wierzchołki na jednostkowym okręgu. Wtedy podczas generowania grafu opisana wyżej modyfikacja to po prostu dodanie pewnego punktu z na okręgu pomiędzy punktami x i y i połączenie go z nimi. Wynika z tego, że w tak wygenerowanym grafie każdy wierzchołek jest zewnętrzny.
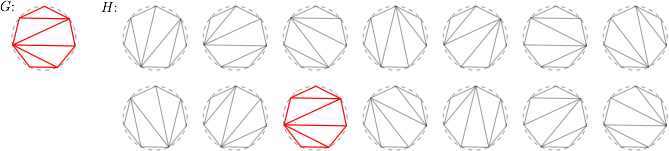
Zastanówmy się teraz jak zdefiniować izomorfizm, tak żeby zrozumiał go pięciolatek. Dobra rada: nie próbujcie używać słowa funkcja. Wystarczy powiedzieć, że trzeba tak poprzesuwać punkty obu grafów (zachowując krawędzie między nimi), żeby wyglądały identycznie. Przesuńmy zatem wierzchołki pierwszego i drugiego grafu do kanonicznej postaci: wierzchołki są na okręgu, kolejne wierzchołki są równoodległe a dodatkowo jeden z wierzchołków znajduje się dokładnie na górze okręgu. Wtedy pierwszy graf G zostawiamy w spokoju, natomiast graf H możemy obrócić na n sposobów lub też odbić lustrzanie otrzymując graf odb(H) i to odbicie obrócić na kolejnych n sposobów. Te sposoby nazywamy orientacjami. Łatwo zauważyć, że G i H są izomorficzne wtedy i tylko wtedy gdy przy jednej z 2n orientacji grafu H rysunki G i H są identyczne. Przykładowe izomorficzne grafy G i H wraz ze wszystkimi orientacjami grafu H przedstawiono poniżej.
Ponieważ sprawdzanie identyczności dwóch rysunków możemy wykonać w czasie liniowym od liczby krawędzi (a więc od n), otrzymujemy algorytm działający w czasie kwadratowym. Jak przyspieszyć powyższy algorytm?Statystycznie może pomóc nam prosta heurystyka. Niech g będzie wierzchołkiem G leżącym na górze okręgu. Wtedy dla konkretnej orientacji grafu H warunkiem koniecznym identyczności rysunków jest to, żeby wierzchołek na górze grafu H miał taki sam stopień jak g. Umożliwia nam to szybkie odrzucanie dużej części rozwiązań. Niestety istnieją przykłady, gdzie taki warunek jest spełniony dla większości orientacji; w takich przypadkach powyższa heurystyka nie przyspieszy znacząco działania. Pójdźmy zatem kawałek dalej i zauważmy, że warunkiem koniecznym identyczności rysunków jest to, żeby stopnie odpowiadających sobie wierzchołków były takie same. Okazuje się, że taka równość jest również warunkiem wystarczającym. Żeby to pokazać, załóżmy że tak nie jest, tzn. że istnieją takie grafy G i H i takie ich orientacje, że listy stopni są takie same, ale rysunki nie są identyczne. Weźmy najmniejszy taki przykład (w sensie liczby wierzchołków). Ze sposobu tworzenia grafu G wynika, że istnieje w nim wierzchołek g o stopniu 2 (np. dodany jako ostatni). Weźmy jego odpowiednik h (również o stopniu 2) w grafie H. Jeśli usuniemy te wierzchołki, zmniejszymy stopień sąsiadujących wierzchołków o jeden, a zatem otrzymamy (mniejsze) grafy G' i H', których listy stopni wierzchołków są identyczne, ale rysunki są nadal nieidentyczne. Otrzymujemy sprzeczność z minimalnością wybranego początkowo przykładu. Dla konkretnej, pojedynczej orientacji grafu H sprawdzenie identyczności listy stopni zajmuje nadal czas liniowy, ale teraz możemy łatwo sprawdzić n orientacji naraz. Wystarczy bowiem sprawdzić, czy listy stopni wierzchołków grafów G i H (lub grafów G i odb(H))są równoważne cyklicznie, tj. czy jedną da się osiągnąć przez cykliczne przesunięcie drugiej. Problem równoważności dwóch napisów v i w o długości n możemy rozwiązać w czasie O(n), sprawdzając na przykład, czy napis v zawiera się w napisie ww. Daje nam to liniowy czas na rozwiązanie całego problemu. Na końcu warto zauważyć, że dane dla tego problemu są podane w postaci listy krawędzi, a do powyższego algorytmu potrzebujemy uporządkowanej listy wierzchołków zewnętrznych. Łatwo ją stworzyć na podstawie listy modyfikacji, która z początkowego trójkąta tworzy wynikowy graf. Zaś taką listę możemy wygenerować w odwróconej kolejności biorąc wynikowy graf (w postaci listy krawędzi) i iteracyjnie usuwając z niego wierzchołki o stopniu 2 aż do otrzymania trójkąta. Jak przechytrzyć testy?Niestety podczas zawodów nie wpadłem na powyższe rozwiązanie. Cóż więc można zrobić, jeśli do końca zawodów zostało 15 minut, a nadal nie wiadomo, jak dobrze rozwiązać zadanie? W przypadku Pogromców Algorytmów, gdzie liczba punktów za zadanie to liczba zaliczonych testów, warto w takim przypadku pokusić się o heurystykę sprawdzającą, czy zachodzi parę warunków koniecznych izomorfizmu. Jeśli któryś z nich nie zachodzi, możemy z czystym sumieniem odpowiedzieć NIE. W przeciwnym wypadku odpowiadamy TAK i liczymy na szczęście lub niefrasobliwość układających testy. Mój program sprawdzał zgodność funkcji Na pierwszą osobę, której uda się znaleźć taki test, czeka nagroda niespodzianka. Wyświetl format pliku wejściowego.
Wejście składa się z opisu dwóch grafów. Każdy graf to liczba wierzchołków n, po której następuje 2 n - 3 par liczb. Każda para to dwa numery wierzchołków (wierzchołki numerowane są od 1 do n). Wszystkie liczby są oddzielone odstępami. Przykładowe wejście to: (3 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com




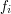 jest po prostu funkcją zwracającą multizbiór tych wartości. Liczba dróg o długości 1 to po prostu stopień wierzchołka, zaś liczbę dróg o długości i zaczynających się w wierzchołku v obliczamy jako sumę liczby dróg o długości i-1 zaczynających się w sąsiadach v.
jest po prostu funkcją zwracającą multizbiór tych wartości. Liczba dróg o długości 1 to po prostu stopień wierzchołka, zaś liczbę dróg o długości i zaczynających się w wierzchołku v obliczamy jako sumę liczby dróg o długości i-1 zaczynających się w sąsiadach v.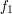 oraz
oraz 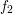 ! Czytelnikowi pozostawiam zadanie ,,poprawienia'' tych testów, tj. znalezienia dwóch nieizomorficznych grafów spełniających warunki zadania, które nie są rozróżniane przez te dwie funkcje. Test można wypróbować wpisując go w ramkę poniżej. Format jest taki sam jak w przypadku jednej instancji w oryginalnym zadaniu.
! Czytelnikowi pozostawiam zadanie ,,poprawienia'' tych testów, tj. znalezienia dwóch nieizomorficznych grafów spełniających warunki zadania, które nie są rozróżniane przez te dwie funkcje. Test można wypróbować wpisując go w ramkę poniżej. Format jest taki sam jak w przypadku jednej instancji w oryginalnym zadaniu.

