Teoria gier, czyli sposób na korki w mieście
03.02.2011 - Krzysztof Dryś
 
John Nash Jr to amerykański matematyk i ekonomista, który
wymyślił i sformalizował teorię gier: matematyczny sposób opisu niewspółpracujących ze sobą graczy.
Cierpiał na schizofrenię paranoidalną.
Historia jego walki z tą chorobą stała się podstawą scenariusza filmu Piękny Umysł.
Teoria gierTeoria gier zajmuje się analizą stanów równowagi (zwanych, od nazwiska twórcy tej teorii, stanami równowagi Nasha). Stan równowagi to taka sytuacja, gdy żadnemu z graczy nie opłaca się zmienić strategii. Gracz to ktoś biorący udział grze. Może to być więzień, firma lub, jak zobaczymy później, człowiek jadący do pracy. Dlaczego analizujemy właśnie stany równowagi? Spróbujmy odpowiedzieć na pytanie: jaka sytuacja w grze (czyli np. na rynku) jest stabilna i nie będzie zmieniać się w czasie? Otóż taka, w której zmiana strategii nie pomoże (nie zwiększy dochodu) żadnemu z graczy. W przypadku Pawła i Gawła jest tylko jeden stan równowagi: gdy obaj na siebie donoszą. W przypadku dwóch firm mamy dwa stany równowagi: jeden, gdy obie firmy sprzedają swój produkt tanio i drugi, gdy obie firmy sprzedają swój produkt drogo.
W tej tabeli widać, że w przypadku dwóch firm są dokładnie dwa stany równowagi:
gdy obie firmy dzielą się zyskiem. Dla łatwiejszej analizy tabeli słowa
tanio i drogo zostały zamienione na konkretne ceny.
Model matematycznyModel matematyczny to próba uproszczonego opisu rzeczywistości. Każdy model ma swoje założenia, które mają oddawać rzeczywistość. Nasz model powinien być na tyle prosty, byśmy umieli wyciągać z niego wnioski i na tyle skomplikowany, żeby te wnioski były zgodne z empirycznymi obserwacjami. W teorii gier próbujemy opisać rzeczywistość właśnie za pomocą gry prowadzonej przez dwie, lub więcej osób. Kolejnym założeniem jest to, że Ci gracze znajdą się w stanie, który jest stanem równowagi. To znaczy, wynikiem gry będzie taka sytuacja, gdy nikomu nie opłaca się zmienić decyzji.
W przykładzie dwóch firm próbowaliśmy opisać skomplikowaną sytuację (rywalizację na rynku) za pomocą bardzo prostego modelu.
Naprawdę, to próbowaliśmy opisać tę sytuację za pomocą macierzy (7 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


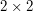 .
Nasz model przewiduje, że obie firmy ustalą tę samą cenę swojego towaru.
Może nie jest to przełomowy wniosek, ale przecież nie można zbyt wiele wymagać od tak prostego
modelu.
.
Nasz model przewiduje, że obie firmy ustalą tę samą cenę swojego towaru.
Może nie jest to przełomowy wniosek, ale przecież nie można zbyt wiele wymagać od tak prostego
modelu.


