Teoria gier, czyli sposób na korki w mieście
03.02.2011 - Krzysztof Dryś
  Kolejna graTeraz zobaczymy inną, bardziej skomplikowaną grę i sprawdzimy, jakie ma ona stany równowagi. Potem zastanowimy się, czy przewidywania tej teorii mają odbicie w rzeczywistości. W pewnym mieście wszyscy jadą z punktu A do B. Średnio w ciągu minuty tę trasę stara się przebyć 4000 samochodów. Przyjmijmy następujące założenia:
Popatrzmy teraz na układ ulic w tym mieście. Widzimy, że mamy dwa rodzaje ulic:
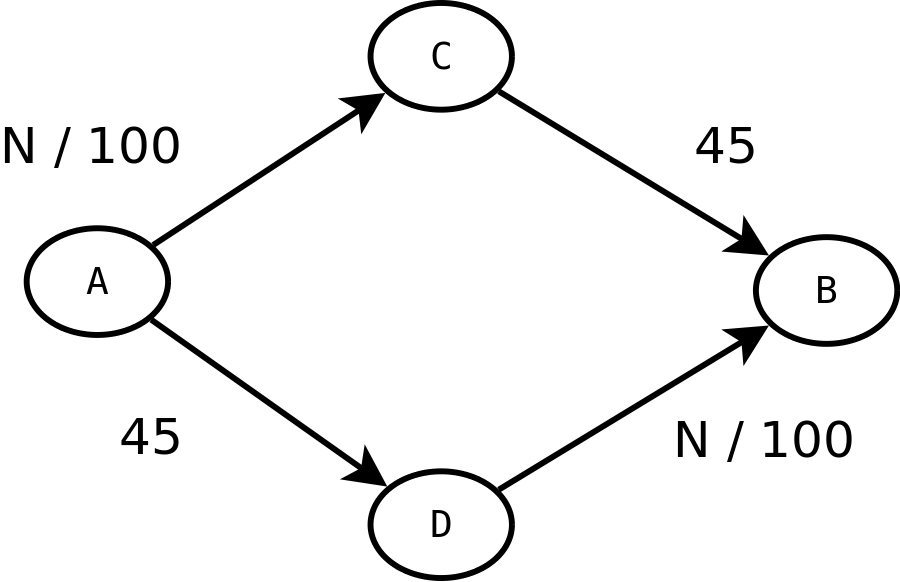 Układ ulic w naszym mieście.
Strzałki reprezentują połączenia, a liczby obok nich pokazują
czas przejazdu (
Układ ulic w naszym mieście.
Strzałki reprezentują połączenia, a liczby obok nich pokazują
czas przejazdu (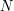 to liczba samochodów jadących ulicą). to liczba samochodów jadących ulicą).
Tak jak poprzednio, zajmiemy się stanami równowagi. Teraz graczami są kierowcy samochodów. Stan równowagi, to takie rozłożenie ruchu, w którym nikomu nie opłaca się zmienić trasy. Można pokazać, że w tym modelu jest tylko jeden stan równowagi. Mianowicie taki, że:
Czas przejazdu każdą z tych tras wynosi 65 minut. Oznacza to, że nasz model przewiduje, że w przy tym układzie ulic przejazd od A do B zajmie właśnie 65 minut. Czas na zmiany!
Teraz dodamy do naszego miasta jeszcze jedną ulicę i zobaczymy
jak zmienią się przewidywania modelu. Nowa ulica będzie
prowadzić od 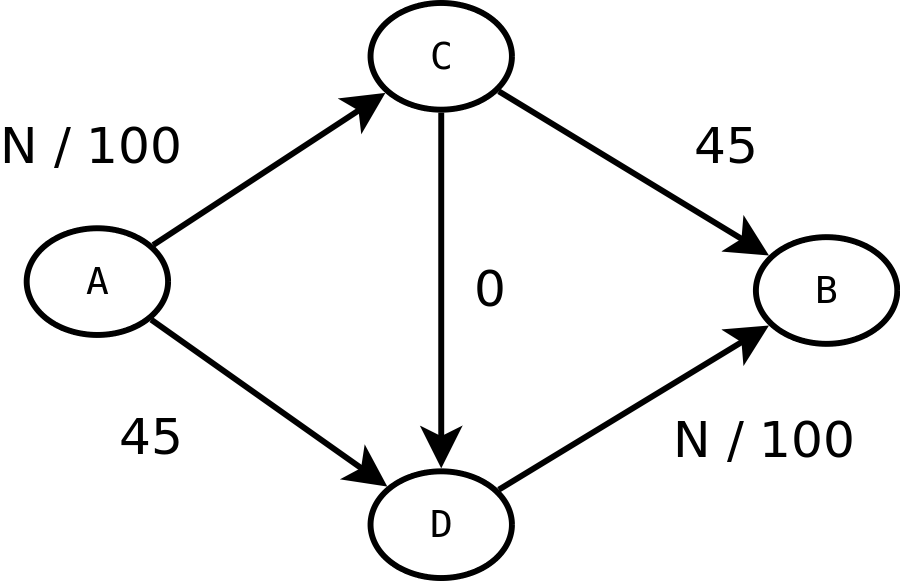 Nowy układ ulic w naszym mieście.
Dodaliśmy połączenie od
Nowy układ ulic w naszym mieście.
Dodaliśmy połączenie od  do do 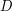 Strzałki reprezentują możlwie połączenia, a liczby obok nich pokazują
czas przejazdu (
Strzałki reprezentują możlwie połączenia, a liczby obok nich pokazują
czas przejazdu (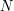 to liczba samochodów jadących ulicą). to liczba samochodów jadących ulicą).
Intuicja podpowiada nam, że jeżeli otworzymy nową ulicę, to czas przejazdu nie powinien spaść. A co mówi nasz model? Przede wszystkim zauważmy, że stan:
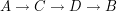 .
Tyle, że ten stan jest mniej korzystny! W tym stanie przejazd samochodem
przez miasto zajmuje 80 minut. .
Tyle, że ten stan jest mniej korzystny! W tym stanie przejazd samochodem
przez miasto zajmuje 80 minut.
Wprowadziliśmy pewien model ruchu samochodów w mieście. W naszym modelu dodanie ulicy może spowodować, że powstanie nowy, mniej korzystny stan równowagi. Oznacza to, że nasz model przewiduje, że dodanie ulicy może spowodować wydłużenie czasu jazdy przez miasto. To zdecydowanie jest sprzeczne z naszą intuicją. Dlatego twierdzenie, że stworzenie dodatkowej drogi może pogorszyć przepustowość, dorobiło się własnej nazwy. Nazywamy je paradoksem Braessa. Paradoks BraessaParadoks Braessa jest przewidywaniem naszego modelu. Przewidywaniem, które jest dla nas niespodziewane. Dlatego od razu nasuwa się pytanie: czy to zjawisko ma miejsce w rzeczywistości? Okazuje się, że tak. Naprawdę zdarza się, że ulice są zamykane po to, by polepszyć warunki jazdy w mieście. Oto parę przykładów.
Ważne jest, żeby mieć świadomość, że powyższy model ma więcej zastosowań niż tylko opis ruchu samochodowego. Może on równie dobrze służyć do opisywania każdej sytuacji, w której różni gracze muszą niezależnie od siebie wybierać drogę. Taką sytuacją jest na przykład internet, gdzie każdy użytkownik chce, by jego pakiety szły najszybszymi (czyli najmniej obciążonymi) łączami. (7 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


 i
i  , wynikające
między innymi z jej długości i jakości nawierzchni,
, wynikające
między innymi z jej długości i jakości nawierzchni, samochodów, to przebycie
tej ulicy zajmuje im
samochodów, to przebycie
tej ulicy zajmuje im 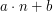 minut.
minut. 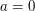 ),
),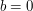 ).
).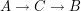 jedzie 2000 samochodów
jedzie 2000 samochodów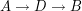 jedzie 2000 samochodów
jedzie 2000 samochodów

