Teoria gier, czyli sposób na korki w mieście
03.02.2011 - Krzysztof Dryś
  Szukamy zastosowańCzy nasz model może się na coś przydać? Zgodnie z tym co zobaczyliśmy wyżej można sądzić, że teoria gier znajduje bezpośrednie zastosowanie przy planowaniu komunikacji w mieście. Można na przykład zastosować poniższy algorytm:
Sprawdź, czy usunięcie tej krawędzi poprawiło przepustowość?
Zgodnie z przewidywaniami naszego modelu należy porównać najgorszy stan
równowagi w wyjściowym grafie z najgorszym stanem równowagi w nowym grafie.
Jeżeli najgorszy stan poprawił się, to możemy założyć, że usunięcie
tej ulicy poprawi komunikację w mieście.
Fakt, że rzeczywistość jest bardziej skomplikowana niż nasz model może i jest
istotny, ale z punktu widzenia matematyka zupełnie nieinteresujący!
Dlaczego jednak ciągle jeździmy po zatłoczonych drogach, skoro powyższy algorytm
mógłby uczynić nasze życie dużo prostszym (i to tylko poprzez zamykanie ulic!)?
Pierwszy powód jest dosyć prosty: nasz model jest dosyć naiwnym opisem rzeczywistości.
Mimo że sprawdza się w prostych przypadkach i poprawnie przewiduje naturę zjawisk, to
już konkretne przewidywania często są zwyczajnie mylne. Ciężko jest na przykład
wyznaczyć stałe
Czym są problemy
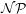 -zupełne? Bardziej niż ich definicja
interesuje nas ich pewna ważna właściwość. Mianowicie nie umiemy
efektywnie (czyli szybko) rozwiązywać tych problemów.
I co więcej: podejrzewamy, że jest to niemożliwe.
Więcej o problemach -zupełne? Bardziej niż ich definicja
interesuje nas ich pewna ważna właściwość. Mianowicie nie umiemy
efektywnie (czyli szybko) rozwiązywać tych problemów.
I co więcej: podejrzewamy, że jest to niemożliwe.
Więcej o problemach  można przeczytać
na
polskiej Wikipedii . można przeczytać
na
polskiej Wikipedii .
Drugi powód ma zupełnie inną naturę. Żeby nasz algorytm dział, musimy
umieć szybko szukać najgorszego stanu równowagi dla zadanego grafu. Jednakże
w grafach, które opisują prawdziwe miasta,
z kierowcami jadącymi różnymi samochodami w różnych kierunkach to zadanie jest bardzo
trudne. Dokładniej mówiąc jest Po co komu teoria gier?W artykule mówiliśmy o bardzo małym wycinku teorii gier. Jednak już ten wycinek jest bardzo interesujący. Dlaczego? Teoria gier jest ciekawaPo pierwsze teorie, które opisywaliśmy są bardzo ciekawe matematycznie. Już w przypadku prostych gier pojawia się wiele ciekawych pytań takich jak:
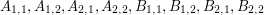 ?
Aby to zrobić możesz podstawiać wartości pod te stałe, napisać program,
który będzie analizował różne przypadki, albo poszukać (i dowieść!) ogólnych
zależności. ?
Aby to zrobić możesz podstawiać wartości pod te stałe, napisać program,
który będzie analizował różne przypadki, albo poszukać (i dowieść!) ogólnych
zależności.
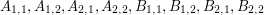 .
W zależności od tego, jak je wybierzemy, nasza gra będzie miała różne
właściwości (np. może mieć, bądź nie mieć stanów równowagi). .
W zależności od tego, jak je wybierzemy, nasza gra będzie miała różne
właściwości (np. może mieć, bądź nie mieć stanów równowagi).
Drugim argumentem za tym, że teoria gier jest interesująca jest to, że pozwala ona tworzyć modele opisujące rzeczywistość. Oczywiście, te modele mogą być mniej lub bardziej dokładne. Ale pozostaje faktem, że biolodzy wykorzystują je do opisu zwierząt w stadzie, a ekonomiści do opisu zachowań firm i konsumentów. Wreszcie, teoria gier jest miejscem ciekawej interakcji pomiędzy informatyką, a pozostałymi dziedzinami nauki. Oczywiście: biolodzy mogą tworzyć modele. Ale przecież ktoś musi pisać programy, które będą liczyły, co te modele przewidują. W przypadku ruchu w mieście musimy wiedzieć, kiedy, dla miasta zadanego grafem, umiemy policzyć najgorszy stan równowagi, kiedy umiemy policzyć jego rozsądne przybliżenie, a kiedy nie umiemy policzyć nic. Wiedzę o tym, jak policzyć przewidywania modelu (i czy jest to w ogóle możliwe) muszą dostarczyć właśnie informatycy. (7 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


 i
i  dla prawdziwych ulic.
dla prawdziwych ulic.
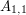 złotych
złotych
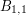 złotych
złotych
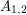 złotych
złotych
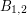 złotych
złotych
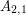 złotych
złotych
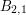 złotych
złotych
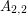 złotych
złotych
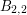 złotych
złotych


