Runda 3 [Hard] - Kokosy
05.12.2010 - Damian Rusak
 
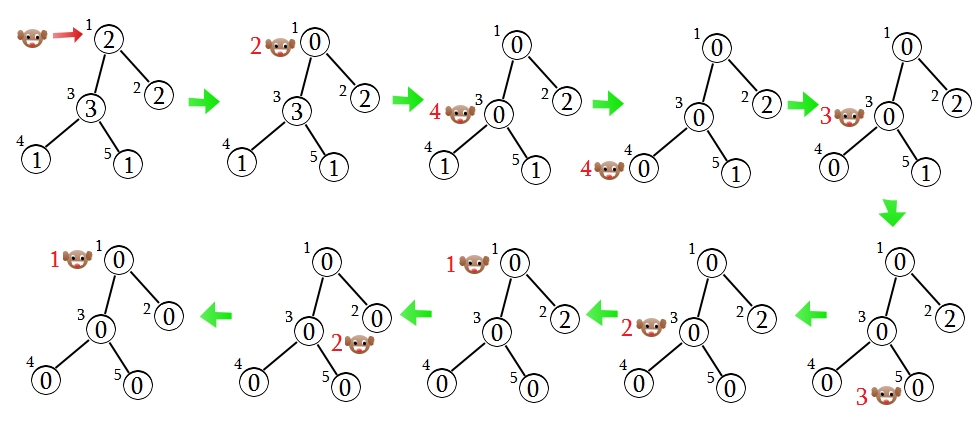
Zadanie tygodnia Runda 3; kategoria Hard Limit czasowy: 1s; Limit pamięciowy: 32MB KokosyW dzikiej dżungli na jednej z odległych wysp na oceanie żyje Małpa. Małpa to przebiegły wielbiciel lokalnych kokosów, które można zebrać z porastających wyspę palm. Jednak jest dla Małpy pewna rzecz, ważniejsza nawet od posiadania kokosów - to pragnienie, aby inne małpy tych kokosów nie miały. Innymi słowy Małpa jest zwierzęcym socjopatą. Małpa dowiedział się, że pozostałe osobniki jego gatunku wybierają się w okolicę wielkiego wulkanu w centrum wyspy, aby oddać cześć przodkom. Postanowił wykorzystać tę okazję, aby ogołocić z kokosów lokalne zbiorowisko palm. Palmy rosną na grząskim piasku i dlatego Małpa może wspinać się na nie tylko po lianach, które łączą niektóre palmy ze sobą, bądź wspiąć się na jedyną palmę, która rośnie na twardym podłożu. Ale co za niespodzianka! "Lianowe" połączenia między palmami tworzą "drzewo" - z każdej palmy można dojść do każdej (być może po drodze poprzez inne palmy) przechodząc po lianach, ale można to zrobić jedynie na jeden sposób. Ponadto wiadomo, że z żadna palma nie jest połączona z więcej niż czterema innymi. Małpa wie, że przejście po każdej lianie jest męczące - musi przed jej przebyciem spożyć jednego kokosa dla wzmocnienia sił, inaczej nie może po niej przejść. Ponadto każda palma obrodziła w tym sezonie w niewielką liczbą kokosów - na każdej z nich rośną jeden, dwa lub trzy kokosy. Małpa zastanawia się, jak zebrać wszystkie kokosy i wrócić na ziemię przez palmę rosnącą na twardym podłożu, jeżeli z owej palmy wystartuje. Wie jedynie, że to możliwe, bo kiedyś jego wujkowi ta sztuka się udała. Małpa zbiera kokosy z palmy, gdy wejdzie na nią po raz pierwszy. Musi jednak najpierw spożyć kokosa na przejście liany, dopiero potem może po owej lianie przejść. Kokosy z palmy, z której Małpa zaczyna, są zbierane przez niego od razu. Wejście: Pierwsza linia wejścia zawiera jedną liczbę naturalną Wyjście: Pierwsza linia wejścia powinna zawierać jedną liczbę całkowitą Przykład: Wejście: 5 2 2 3 1 1 1 3 3 4 3 5 1 2 Wyjście: 9 1 3 4 3 5 3 1 2 1 Wyjaśnienie: Poniższa ilustracja obrazuje jak Małpa chodzi po palmach i jego kokosowy stan posiadania:
Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto.
(1 ocena) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com



 - liczbę palm (
- liczbę palm (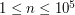 ). Palmy numerowane są od
). Palmy numerowane są od  do
do 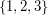 - kolejno liczba kokosów na kolejnych palmach (pierwsza liczba dotyczy palmy nr 1, druga palmy nr 2 itd.). W kolejnych
- kolejno liczba kokosów na kolejnych palmach (pierwsza liczba dotyczy palmy nr 1, druga palmy nr 2 itd.). W kolejnych 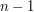 liniach znajdują się pary liczb
liniach znajdują się pary liczb 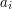
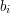 oznaczające, że palmy o tych numerach połączone są lianą. Żadna palma nie pojawi się w więcej niż czterech parach.
oznaczające, że palmy o tych numerach połączone są lianą. Żadna palma nie pojawi się w więcej niż czterech parach. - długość ciągu kolejnych przebywanych przez Małpę palm. W kolejnej linii winno znajdować się
- długość ciągu kolejnych przebywanych przez Małpę palm. W kolejnej linii winno znajdować się