Runda 2 [Hard] - Zające
29.11.2010 - Damian Rusak
 
Zadanie tygodnia Runda 2; kategoria Hard Limit czasowy: 3s; Limit pamięciowy: 64MB ZająceZając Alfred jak co dnia wybrał się na poszukiwanie pokarmu dla grona swoich potomków. Kilkoro zajączków czeka na upragnione kawałki marchewki. Alfred zna pewne pole uprawne, z którego regularnie podkrada marchewkę. Pole podzielone jest na kilka grządek - na każdej z nich rosną marchewki pewnej jednolitej odmiany (odmiany dla różnych grządek mogą być różne). Dla każdej grządki Alfred wie już z doświadczenia, dla ilu jego dzieci wystarczy jedna z marchewek na niej rosnących. Dzieci Alfreda zawsze jedzą tyle samo. Alfred nie chce zabierać więcej marchewek niż jest to konieczne - nie ma sensu zbytnio denerwować właścicieli pola. Postanowił więc zebrać tyle marchewek, aby dokładnie nakarmić siebie i swoje dzieci (możemy uznać, że Alfred konsumuje tyle samo marchewki co dwójka jego dzieci) i nie zostawić żadnych resztek. Alfred woli nie zbierać zawsze tych samych marchewek z tych samych grządek, aby nie wzbudzić podejrzeń gospodarza. Zastanawia się, na ile sposobów może to zrobić. Marchewki z jednej grządki są rozróżnialne, choć kolejność ich wyboru nie ma znaczenia (i tak przemieszają się przy posiłku). Pomóż swojemu futerkowemu przyjacielowi i napisz program, który rozwiąże problem dręczący Alfreda. Wejście: Pierwsza linia wejścia zawiera jedną liczbę całkowitą Wyjście: Jedyna linia wejścia zawierać powinna jedną liczbę całkowitą - liczbę sposobów na które Alfred może zebrać marchewki z grządek tak, aby dokładnie wykarmić siebie i wszystkie zajączki i nie zostawić żadnych resztek. Wynik podaj modulo Przykład: Wejście: 4 3 3 1 4 2 2 5 Wyjście: 28 Mamy do uzbierania 4 + 2 porcje marchewki (czworo dzieci plus ojciec liczący się za dwa).
Można uzbierać 6 na trzy sposoby: 1 + 1 + 2 + 2 (3 sposoby * 6 sposobów = 18) 1 + 5 (3 sposoby * 2 sposoby = 6) 2 + 2 + 2 (4 sposoby) w sumie 28 Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto.
(1 ocena) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com



 - liczbę potomków Alfreda (
- liczbę potomków Alfreda (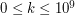 ). W kolejnej linii wejścia znajduje się liczba grządek z marchewką -
). W kolejnej linii wejścia znajduje się liczba grządek z marchewką -  (
(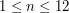 ). W kolejnych
). W kolejnych 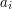
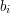 - (
- (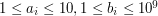 ) odpowiednio liczba marchewek rosnących na
) odpowiednio liczba marchewek rosnących na  -tej grządce, oraz liczba zajączków, które można wykarmić jedną marchewką z tej grządki.
-tej grządce, oraz liczba zajączków, które można wykarmić jedną marchewką z tej grządki.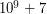 .
.

