Runda 1 [Basic] - Wzgórza
22.11.2010 - Damian Rusak

Zadanie tygodnia Runda 1; kategoria Basic Limit czasowy: 2s; Limit pamięciowy: 64MB
WzgórzaMały Staś bardzo lubi wędrować po górach. Uwielbia zwłaszcza wejść na szczyt jakiegoś wzgórza i podziwiać okolicę. Czasem, gdy ma więcej energii, ma ochotę wspiąć się na najwyższe z okolicznych wzgórz. Innym razem, zmęczony godzinami gry na fortepianie ma siłę wspiąć się tylko na najniższe ze wzgórz. Pomóż Stasiowi i wskaż mu te dwa miejsca na jego mapie okolicy. Mapa okolicy sporządzona jest w szczególny sposób - okolica została podzielona w prostokąt rozmiaru Wejście: Pierwsza linia wejścia zawiera dwie liczby naturalne Wyjście: Na wyjściu w jednym wierszu powinny znaleźć się dwie liczby całkowite - odpowiednio wysokość najwyższego i najniższego ze wzgórz na mapie. Możesz założyć, że na każdej mapie pojawi się co najmniej jedno wzgórze. Przykład: Wejście: 4 5 2 5 5 5 5 1 2 5 6 6 4 3 4 2 1 1 2 2 2 3 Wyjście: 4 3 Na podanej mapie znajdują się dwa wzgórza - jedno w trzecim rzędzie i pierwszej kolumnie, o wysokości 4, oraz w czwartym wierszu i piątej kolumnie o wysokości 3. Pozostałe pola zawsze sąsiadują z pewnym polem o co najmniej takiej samej wysokości, nie spełniają więc definicji wzgórza. Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto.
|
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com



 na
na  , składający się z kwadratów rozmiaru
, składający się z kwadratów rozmiaru  na
na 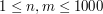 ), oznaczające liczbę wierszy i kolumn opisu mapy. W kolejnych
), oznaczające liczbę wierszy i kolumn opisu mapy. W kolejnych  do
do 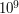 - wysokości kolejnych pól w danym wierszu.
- wysokości kolejnych pól w danym wierszu.

