Runda 0 [Hard] - Niebezpieczne ścieżki
15.11.2010 - Damian Rusak
  Zadanie tygodnia Runda 0; kategoria Hard Limit czasowy: 2s; Limit pamięciowy: 128MB
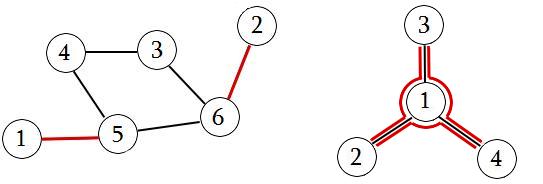
Niebezpieczne ścieżkiJest burzliwa jesień na dalekiej prowincji. Baytard, syn lokalnego bankiera i znany awanturnik kupił właśnie nowy samochód wyścigowy. Zamierza jeździć nim po okolicznych miastach. Lokalne miejscowości połączone są siecią dróg. Drogi są dwukierunkowe. Baytard gardzi jeżdżeniem po bezpiecznych ulicach. Pragnie podróżować jedynie niebezpiecznymi ścieżkami. Jak one wyglądają? Otóż Baytard stwierdził, że najwięcej emocji sprawi mu podróż po drogach, na których wypadek byłby naprawdę spektakularny. Powiemy, że droga między dwoma miastami jest niebezpieczna jeśli wypadek na niej (czyli zablokowanie tej drogi) sprawiłby, że po sieci lokalnych dróg nie dałoby się przejechać (przez pośrednie miejscowości) pomiędzy parą miast, połączonych zablokowaną drogą. Niebezpieczna ścieżka to ścieżka prosta (bez powtarzających się krawędzi), która składa się wyłącznie z niebezpiecznych dróg. Ponadto Baytard, nie chcąc być oskarżonym o tchórzostwo, chce wybrać taką ścieżkę, której nie dałoby się przedłużyć w żadną ze stron o kolejną niebezpieczną drogę. Na ile sposobów może wybrać taką niebezpieczną ścieżkę? Wejście: Pierwsza linia wejścia zawiera dwie liczby Wyjście: Jedyna linia wyjścia powinna zawierać jedną liczbę całkowitą - liczbę nieprzedłużalnych niebezpiecznych ścieżek. Przykład 1: Wejście: 6 6 6 5 4 5 2 6 1 5 3 4 6 3 Wyjście: 2 Przykład 2: Wejście: 4 3 1 2 1 3 1 4 Wyjście: 3 Na poniższych rysunku na czerwono są zaznaczone nieprzedłużalne niebezpieczne ścieżki dla obu przykładów (dla pierwszego 1-5 oraz 2-6, dla drugiego 2-1-3, 2-1-4, 3-1-4):
Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto. |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com



 i
i  , oznaczające kolejno liczbę miast i liczbę dwukierunkowych dróg między nimi (
, oznaczające kolejno liczbę miast i liczbę dwukierunkowych dróg między nimi (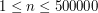 ,
, 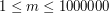 ). W kolejnych
). W kolejnych  i
i  oznaczające, że miasta o numerach
oznaczające, że miasta o numerach