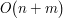Porównywanie ofert

Rozwiązania nadesłane do tego zadania w wiekszości miały dobre intencje, jednak nie zawsze były poprawnie zaprogramowane. Zdarzyły się też zgłoszenia które, zamiast skorzystać z pomysłu (o którym niżej), opierały się na bardzo skomplikowanych i nieadekwatnych do zadania strukturach z biblioteki standardowej. Nie uzyskały one maksymalnej ilości punktów.

Na wejściu dane były dwa zbiory w porządku rosnącym. Należało wypisać ich sumę, iloczyn oraz różnicę symetryczną (tak fachowo nazywają się operacje opisane w zadaniu). Algorytm wzorcowy jest w istocie delikatnie przerobioną procedurą merge ze znanego algorytmu sortującego MergeSort (sortowanie przez scalanie). Ponieważ kilku zawodnikom udało się zaimplementować rozwiązanie wzorcowe, postanowiliśmy ujawnić, dlaczego ono działa, zachowując przy tym pewną dozę precyzji (czyli unikając nadużywania zaimków rzeczownych, przymiotnych i przysłownych). Czytajcie powoli i uważnie.

Oznaczmy pierwszy zbiór przez P, a drugi przez Q. Połóżmy palec (wskaźnik) p na ciągu opisującym zbiór P oraz palec q na ciągu opisującym zbiór Q. Oznaczmy wartości, na które wskazują palce przez odpowiednio *p oraz *q, natomiast wartości, które znajdują się w ciągach P oraz Q bezpośrednio przed *p oraz *q jako odpowiednio _p oraz _q.

Na razie palce znajdują się na początku ciągów, więc wartości _p oraz _q nie istnieją - nie szkodzi. Jednak o ile któraś z tych wartości istnieje, musi zachodzić _p < *p oraz _q < *q (ponieważ ciągi P oraz Q są uporządkowane rosnąco). Zażądajmy również, aby przez cały czas działania algorytmu zachodziło _q < *p oraz _p < *q - na razie nie jest to problem, gdyż ani _p ani _q nie istnieją. Później będziemy starali się o to, aby zależność ta zachodziła - będzie ona bardzo ważna w analizie algorytmu.

Przyjrzyjmy się teraz wartościom *p oraz *q. Może zajść jeden z trzech przypadków:

1. *p < *q: w tym wypadku mamy gwarancję, że wartość *p nigdy nie wystąpi w ciągu Q. Dlaczego? Oczywiście wartość pod wskaźnikiem q jest większa od *p, a wszystkie dalsze wartości w ciągu Q są większe od *q, a zatem także od *p. Wartość _q (bezpośrednio poprzedzająca *q) albo nie istnieje (a zatem nie jest równa *p), albo jest mniejsza od *p - zażądaliśmy tego na wstępie.
   Zatem wartość *p wystąpiła w dokładnie jednym ze zbiorów P, Q. Dopisujemy ją do sumy oraz różnicy symetrycznej zbiorów.
   Następnie przesuwamy wskaźnik p o jedną pozycję do przodu. Pamiętamy przy tym o zależnościach, które sobie przyjęliśmy. Jak się okazuje, pozostaje ona prawdziwa. Było *p < *q. Jeżeli przesunęliśmy wskaźnik p o jedną pozycję do przodu, to _p ma teraz wartość, którą przed chwilą miało *p. Ponieważ przed chwilą zachodziło *p < *q, teraz zachodzi _p < *q, czyli nasza zależność pozostaje spełniona. Była też drugia zależność: _q < *p, która jeszcze przed chwilą była prawdziwa. Po przesunięciu p o jedną pozycję do przodu, wartość *p zwiększyła się (ponieważ ciąg P jest uporządkowany rosnąco) - a zatem zależność _q < *p również pozostała w mocy.
2. *p > *q: podobnie jak wyżej, lecz tym razem wartość *q występuje w tylko jednym ze zbiorów. Przesuwamy palec q.
3. *p = *q: w tym przypadku widzimy, że ta sama wartość występuje w obu zbiorach Dopisujemy ją do sumy oraz iloczynu zbiorów i przesuwamy oba palce o jedną pozycję do przodu. Ponieważ ciągi P oraz Q są uporządkowane rosnąco, nasze zależności pozostają prawdziwe. _p przyjmuje wartość, którą przed chwilą miało *p, które było równe *q. Natomiast nowa wartość *q jest większa od starej, zatem zachodzi _p < *q. Analogicznie rozumując pozostaje prawdziwa zależność _q < *p.

Powtarzamy powyższe operacje dopóki jeden z palców nie wyjdzie poza granicę swojego ciągu. Załóżmy, że palec p wyszedł poza granice P. W takim wypadku _p ma wartość ostatniej liczby w zbiorze P. Wartość *q jest większa od _p (jest to nasza nieśmiertelna zależność) a wszystkie następne wartości w Q są większe od *q (gdyż Q jest uporządkowany rosnąco). Zatem są też większe od _p, a przez to również od wszystkich innych wartości w P. Widzimy zatem, że wartości pozostałe w ciągu Q występują tylko w nim i dopisujemy je do sumy oraz różnicy symetrycznej zbiorów. Analogicznie rozumujemy jeżeli palec q (a nie p) wyjdzie poza granice swojego ciągu.

Przedstawione rozumowanie wykorzystuje niezmiennik - niezwykle ważne narzędzie w analizie algorytmów. Rozpoczynając analizę zauważyliśmy pewną własność (_p < *q, _q < *p), która w danej chwili była prawdziwa. Konstruując algorytm zadbaliśmy o to, aby w każdym jego kroku własność ta pozostawała prawdziwa, dzięki czemu mogliśmy (właściwie to algorytm mógł) z niej korzystać przy podejmowaniu decyzji.

Przyjmując (podobnie jak w zadaniu) za ilość elementów w zbiorze P oraz za ilość elementów w zbiorze Q, spróbuj udowodnić, że powyższe rozwiązanie ma złożoność

Wiktor Janas