Wprowadzenie do zachłanności i dynamiki
18.10.2010 - Łukasz Zatorski
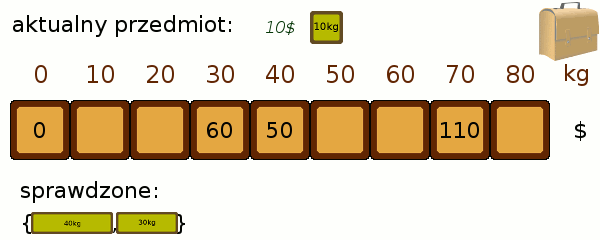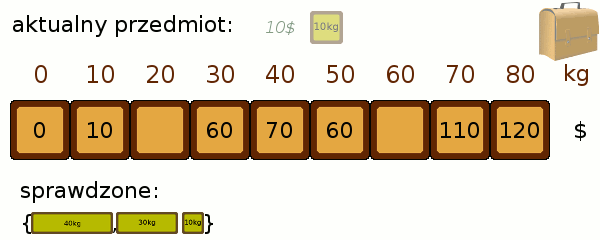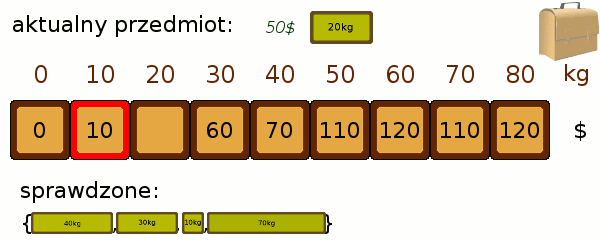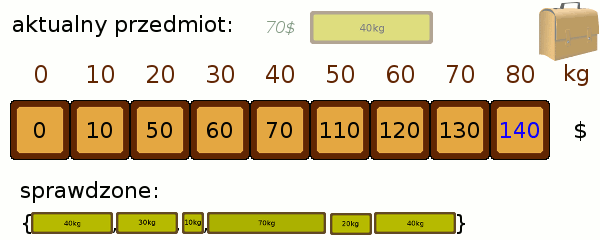
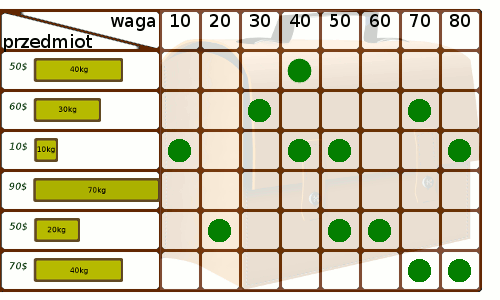
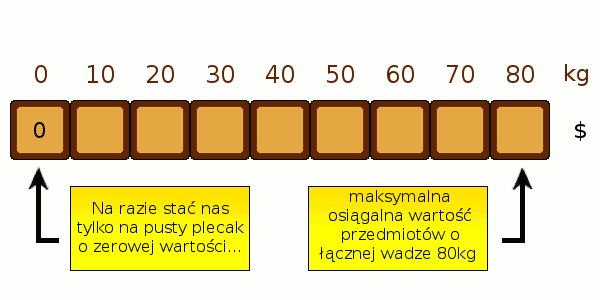
 Podejście dynamicznePomysł jest następujący - spróbujmy podzielić nasz problem na mniejsze, i stopniowo obliczać je by otrzymać upragniony rezultat. Załóżmy, że wagi przedmiotów są liczbami całkowitymi, tak jak w naszym przykładzie. Nie jest to szczególnie nieżyciowe uproszczenie. Jeśli w praktyce dysponujemy wagą z dokładnością do 3 miejsc po przecinku, wystarczy przemnożyć wszystkie jej wskazania przez 1000. Czym w takiej sytuacji będą podproblemy? Dla danego zbioru przedmiotów i każdej możliwej wagi będziemy chcieli wiedzieć jak najlepiej zapakować plecak przy pomocy tych przedmiotów, by osiągnąć dokładnie tę wagę. Najłatwiej będzie to zrozumieć na rysunku - Każde pole odpowiada danemu stanowi zapełnienia, a jego zawartość – najlepszemu osiągniętemu wynikowi (pole puste oznacza, że nie jest możliwe dobranie podzbioru przedmiotów o dokładnie takiej wadze). Będziemy stopniowo rozszerzać zbiór łupów, który bierzemy pod uwagę. Na samym początku nie mamy żadnego przedmiotu – potrafimy zatem mieć pusty plecak o zerowej wartości:
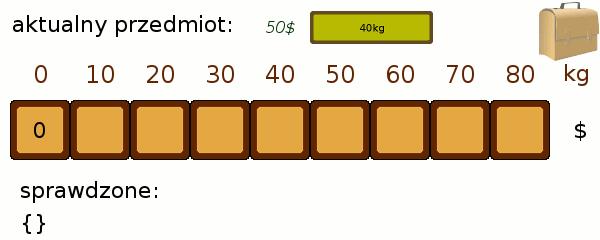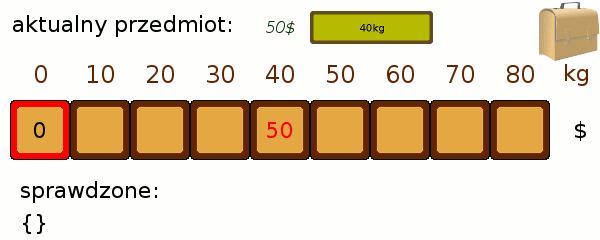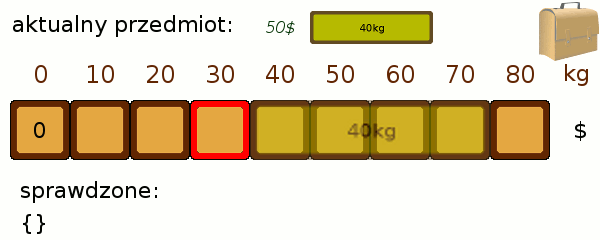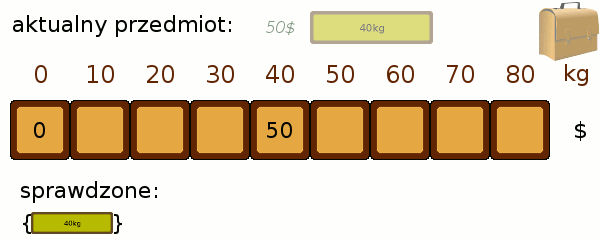
W jaki sposób wypełnić pola poprawnymi wartościami? Będziemy brać przedmioty po kolei, i dokładając do naszego zbioru, poprawiać osiągnięte stany. Wygląda to trochę tak jak dopasowywanie od góry naszego przedmiotu do kolejnych poziomów zapakowania:
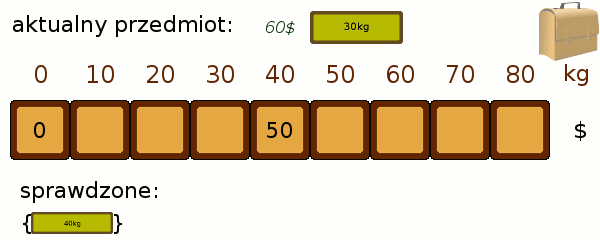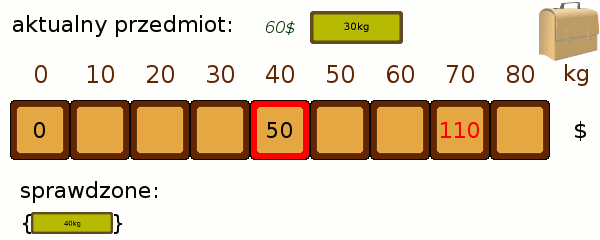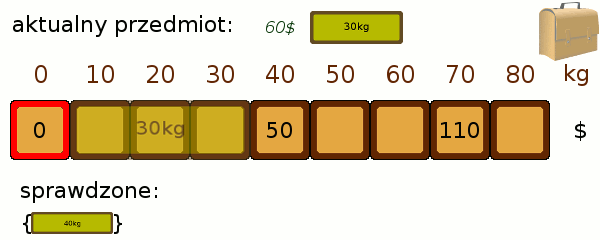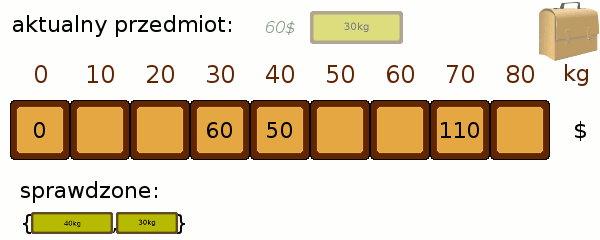
Teraz próbujemy dopasować jeden przedmiot więcej i sprawdzić, czy czasem nie poprawi on nam któregoś z wyników. Przeglądamy po kolei każdy ze stanów. Jeśli udało nam się zapakować plecak do poziomu 40 kg tak, by był wart 50$, a kolejny przedmiot waży 30kg i jest wart 60$, to oznacza, że możliwe jest zapakowanie do poziomu 40+30=70 kg o wartości 50$+60$ = 110$. Porównujemy zatem wartość 110$ z tym, co do tej pory znajdowało się w polu odpowiadającym 70kg i przepisujemy większą z nich. Poniższa animacja prezentuje zastosowanie metody:
Dlaczego to działaDowód poprawności naszego rozwiązania jest bardzo intuicyjny i oparty na prostej indukcji matematycznej. Po każdym przejrzeniu tabeli znajdują się w niej najlepsze wyniki upakowania 0, 10, 20, 30.. kg przy pomocy rozważonych do tej pory przedmiotów. Sytuacją bazową jest pusty plecak. Kiedy do zbioru przedmiotów dokładamy jeszcze jeden, dla każdego stanu mamy do czynienia z dwoma przypadkami:
By w pełni zrozumieć mechanizm działania przyjrzyjmy się jeszcze dalszemu przebiegowi rozwiązania dla naszego przykładu:
Odzyskiwanie wynikuNajlepszym osiągalnym wynikiem jest oczywiście największa z wartości znajdujących się w tablicy - niekoniecznie w ostatniej komórce! Optymalne rozwiązanie nie musi być równoznaczne z pełnym plecakiem. Często interesuje nas sama wartość, chcielibyśmy jednak móc odzyskać informacje, które łupy należałoby wybrać. W tym celu równolegle do prowadzonych przez nas obliczeń uzupełniamy tabelkę, zaznaczając dla kolejnych przedmiotów czy użyliśmy ich do poprawienia rozwiązania, czy też nie - zaznaczając pole za każdym razem, gdy dokonaliśmy edycji któregoś ze stanów:
(13 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


 kg a przedmiot waży
kg a przedmiot waży 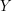 kg, to w takim razie pozostałe przedmioty to takie, które najlepiej pakują
kg, to w takim razie pozostałe przedmioty to takie, które najlepiej pakują 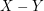 kg.
kg.