Wprowadzenie do zachłanności i dynamiki
18.10.2010 - Łukasz Zatorski
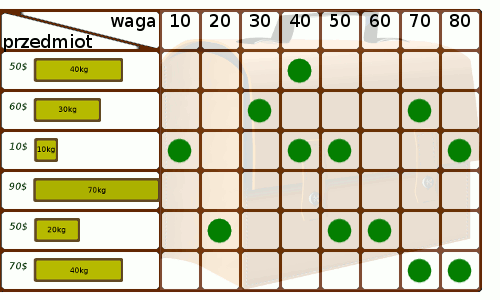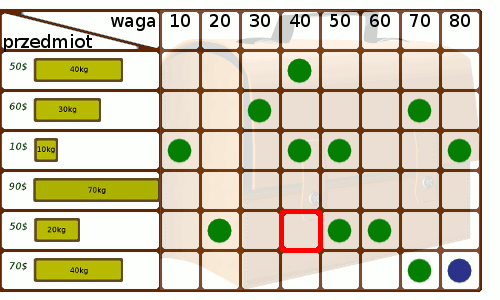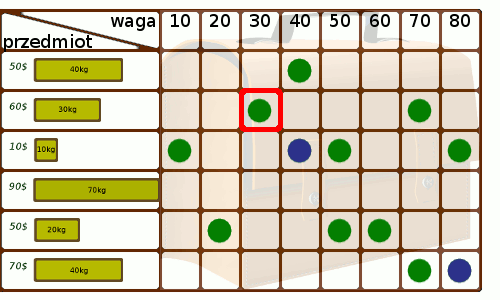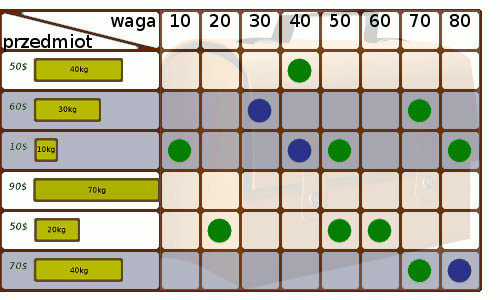
 Kiedy tablica będzie już gotowa, poruszamy się po niej wg następujących reguł:
Poniższa animacja przedstawia przebieg naszego algorytmu dla danych z przykładu:
Taką metodę, w której każdy podproblem liczymy tylko jeden raz nazywamy czasem programowaniem dynamicznym. Termin ten niekoniecznie musi mieć związek z komputerami – powstał on jeszcze przed popularyzacją języków programowania, i chodzi w nim bardziej o podejście – planowanie, niż o konkretną implementację. Nie mniej, rozwiązywanie tego problemu za każdym razem na kartce jest wysoce nieefektywną i żmudną pracą. Stąd programowanie dynamiczne bardzo często stosuje się w algorytmice. Zazwyczaj kod takiego rozwiązania nie wymaga żadnych zaawansowanych struktur danych – wystarczą przemyślane tablice (reprezentujące nasze pola) i pętle (które odpowiadają naszym czynnościom), co ilustruje poniższy pseudokod:
Bardzo ważne jest, by druga pętla przechodziła pola w porządku malejącym – w przeciwnym wypadku korzystając z jednej tablicy mogłoby się zdarzyć, że jakiś przedmiot policzymy więcej niż jeden raz! Dla Ambitnych:Jaki jest czas działania tego problemu? Dwie proste pętle nie sprawiają kłopotów z oszacowaniem złożoności przez Pełne zrozumienie programowania dynamicznego wymaga wprawy – z czasem okazuje się ono doskonałym sposobem rozwiązywania innych problemów optymalizacyjnych. (13 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


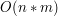 gdzie
gdzie  to ilość przedmiotów, a
to ilość przedmiotów, a  rozmiar plecaka. Nie jest to jednak typowy algorytm wielomianowy – w ogólnym przypadku pojemność plecaka mogłaby bowiem zależeć wykładniczo od wielkości wejścia! W praktyce często nasze plecaki są niewielkie i dlatego podejście dynamiczne jest takie popularne i uznawane za wydajne. Zastanów się nad zmodyfikowaniem tej metody w taki sposób, by radziła sobie z dużymi wagami przy niewielkich ilościach przedmiotów (być może przyda się jakaś struktura danych inna niż tablica).
rozmiar plecaka. Nie jest to jednak typowy algorytm wielomianowy – w ogólnym przypadku pojemność plecaka mogłaby bowiem zależeć wykładniczo od wielkości wejścia! W praktyce często nasze plecaki są niewielkie i dlatego podejście dynamiczne jest takie popularne i uznawane za wydajne. Zastanów się nad zmodyfikowaniem tej metody w taki sposób, by radziła sobie z dużymi wagami przy niewielkich ilościach przedmiotów (być może przyda się jakaś struktura danych inna niż tablica). 

