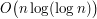Żmudne dzielenie
02.06.2009
 Zadanie to cieszyło się największą popularnością podczas pierwszej rundy, okazało się też zadaniem najtrudniejszym. Ostatecznie tylko pięciu osobom udało się uzyskać za nie maksymalną ilość punktów. Przypomnijmy treść zadania: Dana jest liczba całkowita z zakresu <2; 8*106>. Należy podzielić ją przez jej najmniejszy dzielnik większy od jedności i powtarzać tę operację tak długo, jak to możliwe. Co bardzo istotne w tym zadaniu, nie wystarczy podać odpowiedzi dla jednej liczby - na wejściu może znaleźć się nawet milion zapytań. Przeanalizujmy prosty przykład: załóżmy, że dane są tylko liczby 53227 oraz 59489. Przypuśćmy, że znaleźliśmy najmniejszy dzielnik pierwszej z nich: jest to 17. Dzielimy wyjściową liczbę przez znaleziony najmniejszy dzielnik i nasz problem redukuje się do szukania najmniejszego dzielnika liczby 3131 (który na pewno będzie niemniejszy niż 17 - dlaczego?). Po zakończeniu przetwarzania tej liczby przechodzimy do następnej danej na wejściu: 59489. Znajdujemy najmniejszy dzielnik: 19, eliminujemy go i znów otrzymujemy 3131: liczbę, którą już przetwarzaliśmy. Nie musimy ponownie wyszukiwać jej najmniejszego dzielnika - możemy mieć go zapamiętanego. W ten sposób oszczędzimy sobie olbrzymiej ilości obliczeń i bardzo przyśpieszymy program. Rozwiązanie wzorcowe działa w następujący sposób: dla każdej możliwej liczby na wejściu (od 2 do 8000000) oblicza i zapamiętuje jej najmniejszy dzielnik. Ta faza obliczeń - niezwiązana bezpośrednio z przetwarzaniem danych wejściowych (w rzeczywistości wykonywana zanim jakiekolwiek dane zostaną wczytane) nazywa się preprocessingiem. Jej istotą jest obliczenie pewnych wielkości, których znajomość później przyśpieszy odpowiadanie na zapytania. Mając zapamiętane najmniejsze dzielniki wszystkich możliwych liczb na wejściu możemy błyskawicznie odpowiadać na kolejne zapytania: przychodzącą liczbę dzielimy przez zapamiętany najmniejszy dzielnik i otrzymujemy nową liczbę, dla której również mamy zapamiętany najmniejszy dzielnik. Jednocześnie dzielniki, które będziemy otrzymywać, będą uporządkowane w kolejności niemalejącej (zastanów się, dlaczego). Pozostaje pytanie: skąd wziąć najmniejsze dzielniki wszystkich ośmiu milionów liczb? Nieocenione usługi w tym względzie odda nam sito Eratostenesa. Rozpocznijmy od początku: liczby 2. Wszystkie liczby parzyste (począwszy od dwójki) dzielą się przez 2. Możemy to śmiało zapamiętać. Liczba 3: oczywiście co trzecia liczba począwszy od trójki dzieli się przez 3. Ale uwaga: liczby takie jak 6, 234, 666 owszem, dzielą się przez 3, ale ich najmniejszym dzielnikiem jest 2, co zapamiętaliśmy w poprzednim kroku. Musimy więc uważać, żeby nie nadpisywać mniejszych dzielników większymi. Liczba 4: ponownie uwaga, najmniejszym dzielnikiem tej liczby jest 2, zatem wszystkie wielokrotności czwórki będa miały za najmniejszy dzielnik - dwójkę. Nie ma potrzeby rozpatrywania co czwartej liczby począwszy od czwórki - wszystkie one zostały już odwiedzone, gdy rozpatrywaliśmy dwójkę. Postępujac tak dalej odnajdziemy najmniejsze dzielniki wszystkich liczb - bardzo ważne jest tylko, aby nie nadpisywać mniejszych dzielników większymi (ze względu na poprawność wyniku) oraz aby nie rozpatrywać liczb, które mają już zapamiętany jakiś najmniejszy dzielnik (ze względu na wydajność programu). Istnieją jeszcze pewna "sztuczka" przyśpieszająca działanie sita Erastotenesa. Załóżmy, że rozpatrujemy liczbę 5 oraz jej wielokrotności: 10 = 2*5, 15 = 3*5, 20 = 4*5, 25 = 5*5. Zauważmy, że pierwsze trzy wielokrotności są iloczynem piątki oraz jakiejś innej, mniejszej liczby - a zatem zostały już odwiedzone! Dziesiątka oraz dwudziestka zostały odwiedzone podczas rozpatrywania wielokrotności dwójki, piętnastka - podczas rozpatrywania wielokrotności trójki. Zatem pierwszą wielokrotnością, jaką chcemy rozpatrzyć dla piątki jest 25 = 5*5. W istocie zawsze kiedy rozpatrujemy liczbę a, pierwszą wielokrotnością, która jeszcze nie została odwiedzona będzie a*a. Bardzo ciekawą konsekwencją tego faktu jest ograniczenie zakresu liczb, które chcemy rozpatrywać - jeżeli interesują nas dzielniki liczb nie większych od ośmiu milionów, a rozpatrując liczbę a rozpoczynamy od jej kwadratu, to nie ma sensu podstawiać za a liczb większych od pierwiastka z ośmiu milionów! Można udowodnić (jakkolwiek nie jest to proste zadanie; wystarczy, że uwierzycie nam na słowo), że złożoność sita Erastotenesa przy zastosowaniu powższych obserwacji wynosi
Napisz program, który używając powyższej meotdy wypisze najmniejsze dzielniki liczb od dwa do 100. Gdzie są wśród nich liczby pierwsze, jak szybko je znaleźć? Jak to się stało? Wiktor Janas (1 ocena) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com