Algorytm Bellmana-Forda
03.10.2010 - Damian Rusak
  Zadania
Najkrótsze ścieżki:Dany jest graf skierowany z wagami na krawędziach. Należy znaleźć najkrótsze ścieżki od wierzchołka startowego do wszystkich pozostałych. Wierzchołki są numerowane od Wejście:Pierwsza linia wejścia zawiera dwie liczby całkowite Wyjście: Jeśli z wierzchołka startowego można osiągnąć cykl ujemny, wyjście powinno składać się jedynie z jednej linii z napisem "cykl ujemny". W przeciwnym razie należy wypisać Przykład 1: Wejście: 8 10 1 2 10 1 3 10 1 6 2 2 5 5 3 2 -9 3 4 -8 3 7 3 5 3 4 5 7 -4 6 7 1 Wyjście: 1 10 2 6 2 2 nieosiagalny Przykład 2: 7 11 1 2 10 1 3 10 1 6 2 2 5 5 3 2 -9 4 1 -4 3 4 -8 3 7 3 5 3 3 5 7 -4 6 7 1 Wyjście: cykl ujemny Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto.
Tor wyścigowyEdward otworzył w Wielkim Mieście ekscytujący Tor Wyścigowy. Tor składa się z mnogości tuneli, łączących stacje pośrednie. Tunele nie przecinają się ani nie łączą poza stacjami pośrednimi, mogą za to przebiegać nad albo pod sobą. Każdy tunel ma przypisaną sobie ilość paliwa, które przejechanie przez ów tunel pochłania. Edward boi się konkurencji, postanowił więc uatrakcyjnić klientom pobyt na torze. Postanowił, że na każdej stacji pośredniej będzie tankował bolidy klientów o określoną ilość paliwa (taką samą dla każdej stacji pośredniej, włączając stację początkową). Pojawia się jednak problem - gdyby ta ilość była za duża mogłoby się zdarzyć, że klient byłby w stanie jeździć bez końca po torze, tankując więcej niż spala w tunelach. Poprosił więc Ciebie o pomoc, aby ustalić, ile co najwyżej paliwa może podarować uczestnikom za każdym razem gdy dojadą na stację pośrednią, tak aby uniknąć tej kłopotliwej sytuacji. Pamiętaj, że klient może jechać po torze, jeśli bilans paliwa równa się zero! (Na przykład wszystkie tunele wymuszają spalenie 4 litrów paliwa, a Edward dolewa 4 litry przy każdej stacji)
Wejście:Pierwsza linia wejścia zawiera najpierw liczbę stacji na torze wyścigowym - Wyjście: Jedyna linia wyjścia winna zawierać jedną liczbę całkowitą Przykład 1: Wejście: 4 4 1 2 4 2 3 4 3 4 4 4 1 5 Wyjście: 4 Objaśnienie: gdyby Przykład 2: Wejście: 5 8 4 1 38 1 2 31 2 3 28 2 5 12 3 1 12 5 3 29 4 2 21 4 3 28 Wyjście: 21
Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto.
(4 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


 do
do  , przy czym wierzchołek startowy ma numer 1.
, przy czym wierzchołek startowy ma numer 1.
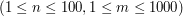 , oznaczające kolejno liczbę wierzchołków i krawędzi w grafie. W kolejnych
, oznaczające kolejno liczbę wierzchołków i krawędzi w grafie. W kolejnych  ,
,  i
i 
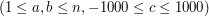 , oznaczające kolejno początek i koniec krawędzi oraz jej wagę.
, oznaczające kolejno początek i koniec krawędzi oraz jej wagę. 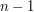 linii, w których zapisane będą najmniejsze odległości kolejno do wierzchołków od numeru
linii, w których zapisane będą najmniejsze odległości kolejno do wierzchołków od numeru 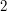 do numeru
do numeru 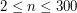 ). Stacje ponumerowane są od
). Stacje ponumerowane są od 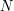 przy czym stacja początkowa ma numer
przy czym stacja początkowa ma numer 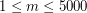 ). Kolejne
). Kolejne 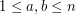 ,
, 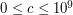 ) - oznaczające, że istnieje jednokierunkowy tunel pomiędzy stacjami
) - oznaczające, że istnieje jednokierunkowy tunel pomiędzy stacjami 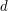 - największą możliwą liczbę litrów paliwa, które można dolewać do baku klienta za każdym razem, gdy wjedzie na jakąkolwiek stację pośrednią (włącznie ze stacją początkową, czyli również przed rozpoczęciem jazdy), taką że uniemożliwi to klientowi nieskończoną podróż po torze. Możesz założyć, że nigdy nie wystąpi sytuacja, w której początkowy uklad tuneli pozwalałby na takie zachowanie.
- największą możliwą liczbę litrów paliwa, które można dolewać do baku klienta za każdym razem, gdy wjedzie na jakąkolwiek stację pośrednią (włącznie ze stacją początkową, czyli również przed rozpoczęciem jazdy), taką że uniemożliwi to klientowi nieskończoną podróż po torze. Możesz założyć, że nigdy nie wystąpi sytuacja, w której początkowy uklad tuneli pozwalałby na takie zachowanie.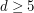 można by jeździć po stacjach 1 -> 2 -> 3 -> 4 -> 1 -> 2 ... bez końca.
można by jeździć po stacjach 1 -> 2 -> 3 -> 4 -> 1 -> 2 ... bez końca.

