Algorytm Bellmana-Forda
03.10.2010 - Damian Rusak
  Optymalne ścieżkiZastanówmy się chwilę nad tym, jak wyglądają najkrótsze ścieżki w grafie. Jeżeli pytalibyśmy nie tylko o najtańsze połączenie między dwoma wybranymi wierzchołkami, ale starali się znaleźć najtańsze połączenie między pewnym wierzchołkiem startowym, a wszystkimi pozostałymi, to szybko zauważymy, że: Jeżeli najtańsza ścieżka do wierzchołka Innymi słowy - najtańsze ścieżki korzystają z krótszych najtańszych ścieżek - gdyby do wspomnianego wierzchołka Jeśli ścieżka
Pozostaje nam jeszcze jedna obserwacja, aby zbliżyć się do algorytmu. Poprzedni pomysł związany z optymalnymi ścieżkami daje nam jedną szczególną własność - jeśli chcemy znaleźć najkrótszą ścieżkę do pewnego wierzchołka, to jakoś ta ścieżka musiała doń "wejść" - musi ona przychodzić od jakiegoś sąsiada. Wobec tego możemy spojrzeć na całą tę sprawę bardziej lokalnie, jak na "podłączanie" się wierzchołków do krótszych ścieżek. Nasze podejście będzie polegało na stopniowym znajdowaniu coraz lepszych ścieżek dochodzących do wszystkich wierzchołków. Poprawianie wynikówJeśli udało nam się znaleźć dobry sposób na dojście do pewnego wierzchołka, to za pomocą tego rozwiązania możemy poprawić rozwiązania dla jego sąsiadów. Jeżeli do wierzchołka
Taką operację będziemy nazywali relaksacją krawędzi. Spójrz na animację poniżej - pokazuje ona jak kolejno można poprawiać odległości do wszystkich wierzchołków. Na początku wszystkie wierzchołki (poza startem, który ma odległość
Relaksacja działaBardzo ważne jest to, że za pomocą relaksacji krawędzi można znaleźć najtańszą ścieżkę od startu do dowolnego innego wierzchołka (cały czas zakładamy, że nie ma w grafie cyklu ujemnego). Oznaczmy wierzchołek początkowy jako Pierwsza relaksacja ustali najtańszą ścieżkę do
(4 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


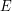 prowadzi przez wierzchołek
prowadzi przez wierzchołek 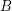 , to początek tej ścieżki, wiodący do
, to początek tej ścieżki, wiodący do  .
. jest droższa niż optymalna ścieżka
jest droższa niż optymalna ścieżka 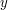 z
z 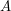 do
do  nie może być optymalna. Musi zawierać optymalne połączenie między
nie może być optymalna. Musi zawierać optymalne połączenie między 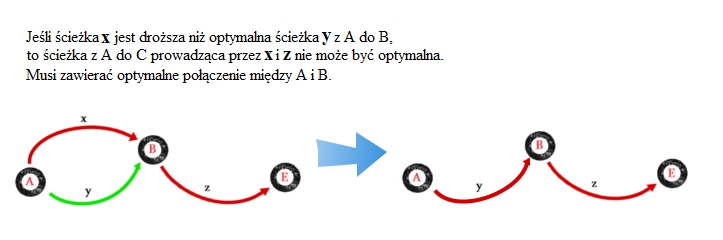
 , to możemy zaproponować dla wierzchołka
, to możemy zaproponować dla wierzchołka 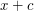 - można wszak poprowadzić ścieżkę do
- można wszak poprowadzić ścieżkę do 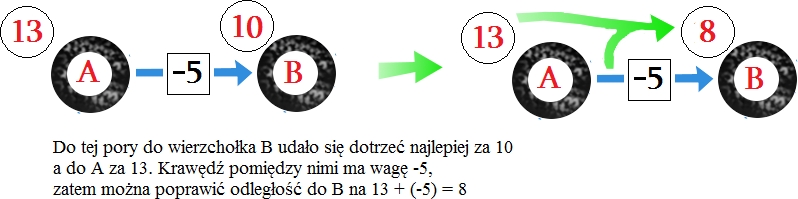
 ) mają odległość ustawioną na
) mają odległość ustawioną na 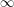 - symbol nieskończoności, oznaczający, że dany wierzchołek jeszcze nie został ani razu odwiedzony. Na czerwono zaznaczane są krawędzie, które są relaksowane, czyli wykorzystane do poprawienia odległości dla wierzchołka, do którego krawędź wchodzi.
- symbol nieskończoności, oznaczający, że dany wierzchołek jeszcze nie został ani razu odwiedzony. Na czerwono zaznaczane są krawędzie, które są relaksowane, czyli wykorzystane do poprawienia odległości dla wierzchołka, do którego krawędź wchodzi.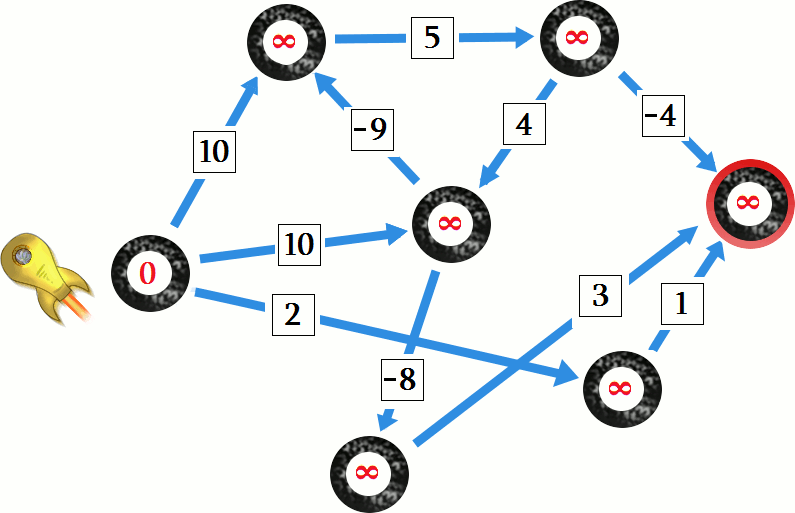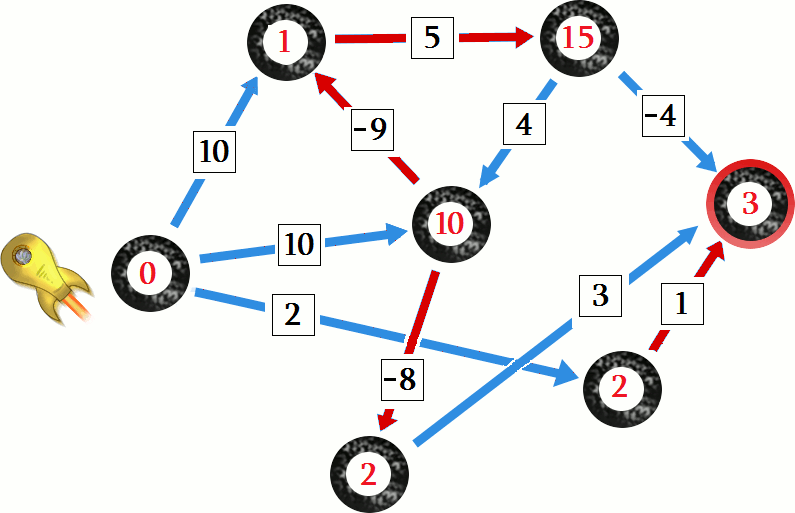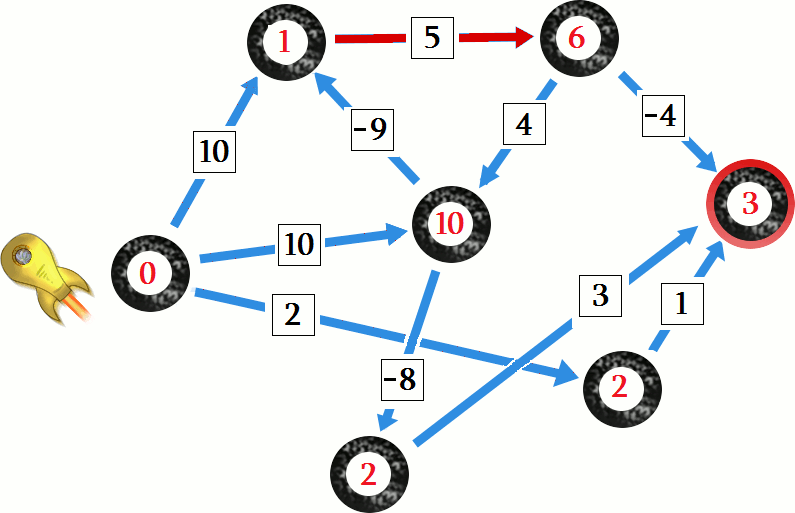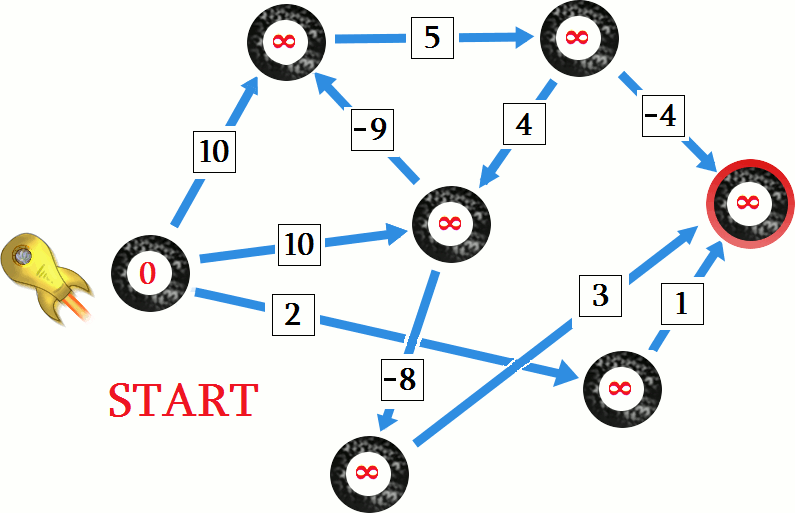
 . Zauważ, że jeśli najtańsza ścieżka z
. Zauważ, że jeśli najtańsza ścieżka z 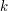 ) do pewnego wierzchołka
) do pewnego wierzchołka  składa się z wierzchołków
składa się z wierzchołków 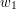 ,
, 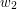 , ...,
, ..., 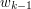 ,
, 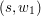 ,
, 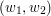 , ... ,
, ... , 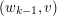 .
. 


