Przeszukiwanie grafu w głąb (DFS)
01.10.2010 - Michał Karpiński
 Ostatnie poprawki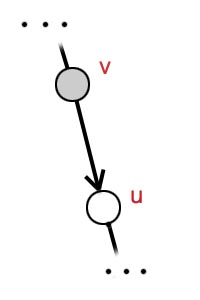
Znamy definicję lasu przeszukiwania w głąb i wiemy jak narysować go na papierze. Kolejne pytanie, które się nasuwa, to: Jak zmodyfikować kod procedury DFS i DFS-ODWIEDZAJ tak, aby zapamiętać drzewa przeszukiwania w głąb? Rozwiązanie jest bardzo proste: wystarczy pamiętać skąd się przyszło. Załóżmy, że podczas przechodzenia po grafie znaleźliśmy się w wierzchołku v. Kolorujemy go na szaro i przeglądamy jego listę sąsiadów. Okazuje się, że wierzchołek u nie został jeszcze odwiedzony. Według dotychczasowej wersji procedury DFS-ODWIEDZAJ po prostu przeszlibyśmy rekurencyjnie do wierzchołka u. Jednak tym razem chcemy zapamiętać dodatkową informację - poprzednika wierzchołka u, czyli wierzchołek, z którego doszliśmy do u. W tym przypadku poprzednikiem wierzchołka u jest wierzchołek v. Fakt ten zapisywać będziemy tak:
Wprowadzamy ostatnie poprawki do pseudokodu:  Dodatkowa instrukcja w procedurze DFS-ODWIEDZAJ nie powinna wprawić nikogo w zakłopotanie - gdy znajdziemy nieodwiedzony wierzchołek, to jego poprzednikiem jest v. Zmiana dokonana w procedurze DFS nie wnosi niczego nowego do algorytmu. Nowa linia kodu wprowadzona została w celach "technicznych". Atrybut p musi posiadać jakąś wartość początkową tzn. chcemy powiedzieć, że przed przystąpieniem do przeszukiwania żaden z wierzchołków nie ma poprzednika. Dlatego ustawiamy wszystkim wierzchołkom specjalną wartość NULL (czyli nic). Przykład zastosowania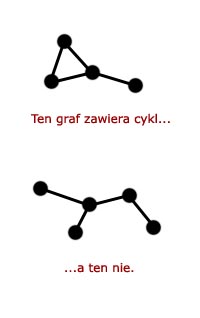
Cyklem w teorii grafów jest droga zamknięta, czyli taka, która rozpoczyna się i kończy w tym samym wierzchołku. Okazuje się, że algorytm przeszukiwania w głąb doskonale nadaje się do stwierdzenia czy podany graf zawiera cykl. Pamiętamy, że podczas przeszukiwania nie wchodzimy do odwiedzonych już wierzchołków, ponieważ istnieje duża szansa, że algorytm się zapętli. Szukając cyklu w grafie skorzystamy z tego faktu. Gdy przechodzimy po grafie najpierw kolorujemy wierzchołki na szaro a później przeglądamy ich listy sąsiedztwa. Co by się stało, gdyby podczas wybierania sąsiada okazało się, że któryś z nich jest pokolorowany na szaro? Odpowiedź nie powinna nikogo zdziwić – właśnie znaleźliśmy cykl. To jest niezwykle proste: skoro będąc w wierzchołku v, jakiś sąsiad u jest szary, to znaczy, że przeszliśmy drogę, która zaczyna się w u i kończy w u. Idealnie pasuje to do definicji cyklu. Jedyną rzeczą, którą trzeba zmienić w algorytmie DFS, żeby mógł wykrywać cykle w grafie jest dodanie jednego warunku do pętli, która przegląda listę sąsiadów danego wierzchołka. Odpowiednie zmiany w poznanych przez nas procedurach pozostawię do wykonania czytelnikowi, jako ćwiczenie. (11 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com




