Przeszukiwanie grafu w głąb (DFS)
01.10.2010 - Michał Karpiński
 Las przeszukiwania w głąbDo tej pory zajmowaliśmy się tylko wierzchołkami, nadając im różne kolory i etykiety. W tym rozdziale będziemy rozważać również krawędzie grafu. Szczególnie interesują nas te krawędzie, po których przechodziliśmy za pomocą algorytmu przeszukiwania w głąb. Łatwo zauważyć, że podczas przechodzenia po grafie, przeszukiwanie nie musi zaczynać się i kończyć tylko w jednym wybranym wierzchołku (patrz: animacja na poprzedniej stronie). Inaczej mówiąc – może istnieć więcej niż jeden wierzchołek startowy. W praktyce, sytuacja gdzie dokonujemy tylko jednego przejścia i udaje nam się przy tym odwiedzić cały graf jest bardzo rzadka. Przeanalizujmy prosty przykład. Załóżmy, że mamy narysowany graf i wybraliśmy dla niego wierzchołek startowy. Wierzchołek ten nazwijmy v1. 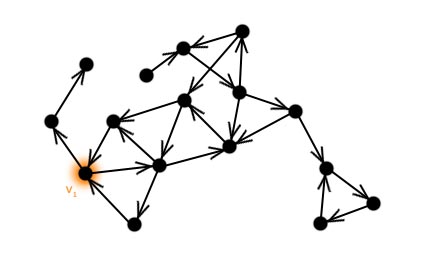 Wykonujemy jedno przejście po grafie zaczynając od wierzchołka v1. Oznaczmy wierzchołki i krawędzie po których przechodziliśmy. 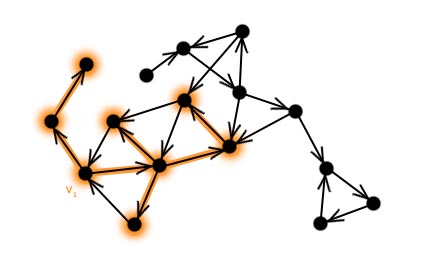 Łatwo zauważyć, że nie przechodziliśmy przez krawędzie, które prowadziły do odwiedzonego już wierzchołka (gdyby było inaczej, to algorytm mógłby się zapętlić). Wierzchołki i krawędzie oznaczone kolorem pomarańczowym na rysunku tworzą drzewo przeszukiwania w głąb. Jak już wspomniane było wcześniej, przeszukiwanie grafu metodą "w głąb" może wykonywać się z wielu źródeł. Wniosek, który płynie z tej obserwacji jest następujący: Drzew przeszukiwania w głąb jest dokładnie tyle, ile jest wierzchołków startowych wybranych podczas działania algorytmu DFS Zbiór wszystkich drzew przeszukiwania w głąb - które zostały utworzone podczas przechodzenia po grafie - nazywamy lasem przeszukiwania w głąb. Znajdźmy taki las w naszym przykładzie. Wybieramy kolejny wierzchołek startowy: 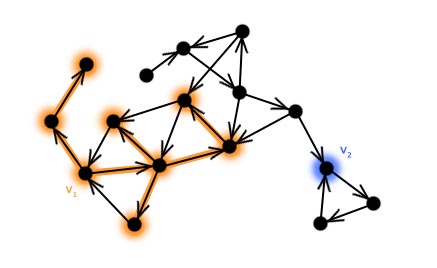 Wykonujemy przejście kolorując przy tym odpowiednie wierzchołki i krawędzie: 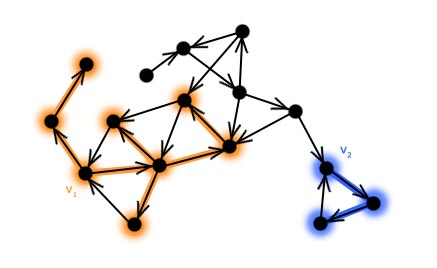 Wybieramy następne źródło: 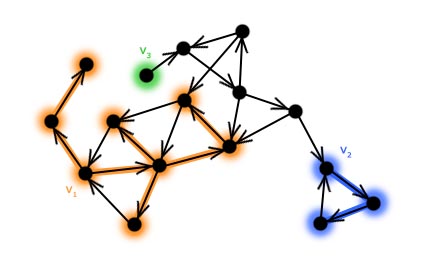 I po raz kolejny przechodzimy po grafie: 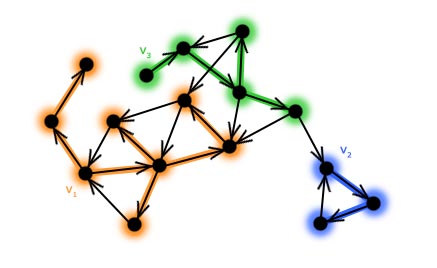 Kończymy przeszukiwanie, gdyż wszystkie wierzchołki zostały odwiedzone. Jak widać na rysunku powyżej - dla tak wybranych wierzchołków startowych - las przeszukiwania w głąb składa się z trzech drzew. Proste pytanie kontrolne: Ile drzew zawierałby las przeszukiwania w głąb dla powyższego grafu, gdyby przeszukiwanie nie rozpoczęłoby się z wierzchołka v1, lecz z v3? (11 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com




