Arkanoid 3D krok po kroku III
02.08.2010 - Olgierd Humeńczuk
  Aktualizacja pozycji aktorówNa początek zaimplementujemy poruszanie się rakietki oraz kuli. Ruch rakietki zależeć będzie od tego, jak mocno gracz poruszy myszką. Kula natomiast poruszać się będzie - na razie - z jednostajną prędkością. Przyjrzyjmy się funktorowi, który obsługiwał będzie aktualizację pozycji aktorów.
Jak widać funktor aktualizujący pozycję aktorów zbudowany jest bardzo prosto. Zależnie od typu aktora, modyfikuje jego pozycję. Dla kuli przesuwa aktualną pozycję w kierunku, w którym wskazuje wektor dir o odległość określoną w zmiennej velocity. Do aktualizacji pozycji rakietki użyliśmy kodu ze starej funkcji main. Niestety taki sposób obliczania aktualnej pozycji nie jest fizycznie poprawny. Nie bierze pod uwagę zmiany czasu. Ulepszaniem tej implementacji zajmiemy się jednak w następnych artykułach, ponieważ został nam do omówienia bardzo ważny dla naszej gry temat wykrywania kolizji.
Wykrywanie kolizji
Podstawowym rodzajem kolizji, jaki będziemy musieli obsługiwać, jest kolizja kuli z różnymi figurami geometrycznymi. Dzięki temu,
że nasza kula porusza się w jednej, stałej płaszczyźnie Aby stwierdzić, czy nastąpiła kolizja kuli z jakimś obiektem, wystarczy sprawdzić, czy okrąg o promieniu kuli przecina się z którąkolwiek krawędzią testowanego obiektu. Wyprowadzimy zatem wzór, który pozwoli nam wyliczyć, czy takie przecięcie nastąpiło. 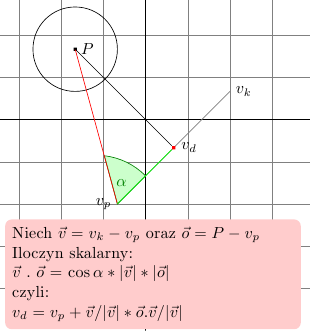 Rys. 6. Wykrywanie kolizji okręgu z odcinkiem.
Wzór przedstawiony na Rys. 6 pozwoli nam na obliczenie długości odcinka pomiędzy punktami
Wzór ten rzutuje wektor
Musimy jednak pamiętać, że nie zawsze punkt Zaimplementujmy zatem funkcję realizującą te obliczenia.
Aby łatwiej zrozumieć działania wykonane w tej funkcji, przypiszmy jej argumentom oznaczenia wprowadzone na Rys. 6.
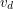 , a w zmiennej offset zwraca przesunięcie środka okręgu,
po zastosowaniu którego okrąg będzie stykał się odcinkiem w prawdziwym punkcie kolizji. , a w zmiennej offset zwraca przesunięcie środka okręgu,
po zastosowaniu którego okrąg będzie stykał się odcinkiem w prawdziwym punkcie kolizji.
Korzystając z tej funkcji, łatwo zaimplementujemy funktor testujący kolizje kuli z poszczególnymi elementami sceny. Ponieważ jest to dobre ćwiczenie, postarajmy się to zrobić samodzielnie. W odnośniku na końcu artykułu znajduje się zwyczajowo archiwum z kompletną implementacją materiału przedstawionego w tym artykule, którą można się posiłkować w razie problemów. Powodzenia !
Zachęcam do przedstawienia swoich rozwiązań na forum, oraz do zadawania pytań dotyczących treści artykułów o tworzeniu naszej gry.
(2 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


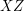 , możemy sprowadzić obliczenia związane z kolizją do tej właśnie płaszczyzny.
To oznacza, że będziemy mogli rozpatrywać kolizje w przestrzeni dwuwymiarowej.
, możemy sprowadzić obliczenia związane z kolizją do tej właśnie płaszczyzny.
To oznacza, że będziemy mogli rozpatrywać kolizje w przestrzeni dwuwymiarowej.
 , gdzie
, gdzie 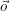 na wektor
na wektor 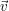 dzięki czemu możemy
obliczyć pozycję punktu
dzięki czemu możemy
obliczyć pozycję punktu 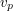 oraz
oraz 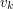 , jednak
znajdował się będzie poza odcinkiem łączącym te punkty. W takim wypadku będziemy musieli użyć odpowiednio: początku odcinka,
czyli punktu
, jednak
znajdował się będzie poza odcinkiem łączącym te punkty. W takim wypadku będziemy musieli użyć odpowiednio: początku odcinka,
czyli punktu 

