Arkanoid 3D krok po kroku III
02.08.2010 - Olgierd Humeńczuk
  A wektory normalne ?No dobrze, wiemy już jak wyznaczać współrzędne wierzchołków. A co z wektorami normalnymi ? W przypadku powierzchni prostopadłych do dowolnej osi układu współrzędnych, nie mieliśmy problemu z ich odgadnięciem. Teraz będziemy musieli je obliczyć. W ramce poniżej znajduje się przepis na obliczanie tzw. uśrednionych wektorów normalnych oraz wynik użycia wektorów normalnych wielokątów i uśrednionych wektorów normalnych dla wierzchołków, do obliczeń związanych z oświetleniem bryły. Więcej o normalnych, o ich obliczaniu i problemach związanych z ich używaniemDo obliczeń związanych z oświetleniem możemy używać wektorów normalnych wielokątów lub wektorów normalnych, pamiętanych w wierzchołkach. W przypadku brył bez gładkich, zaokrąglonych powierzchni, takich jak np. prostopadłościan, nie będzie widać różnicy. Jednak dla brył takich jak sfera, różnica w wynikowym obrazie będzie ogromna. Co można zaobserwować porównując Rys. 4. i Rys. 5. 
Rys. 4. Rendering sfery z użyciem normalnych wielokątów. 
Rys. 5. Rendering sfery z użyciem uśrednionych normalnych. Zawsze znajdzie się jakieś "ale". Decydując się na użycie wektorów normalnych uśrednionych oraz przechowując je w strukturze wierzchołków, czyli tak jak my to robimy, musimy uważać używając tzw. list sąsiedztwa wierzchołków. Zadaniem tych list jest przechowanie informacji o kolejności, w jakiej powinny być przetwarzane wierzchołki. Wierzołki w liscie sąsiedztwa mogą się powtarzać.
Powszechnie używa się list sąsiedztwa, aby zminimalizować liczbę wierzchołków podawanych akceleratorowi.
Dzięki użyciu takich list bylibyśmy w stanie zredukować
liczbę wierzchołków naszej sfery z Listy sąsiedztwa uniemożliwiają jednak użycie uśrednionych normalnych do modelowania brył posiadających ostre krawędzie. Wszędzie tam, gdzie takie krawędzie występują, dubluje się wierzchołki i przypisuje się im różne normalne. W większości przypadków, jeżeli wektory normalne nie są znane, algorytm ich obliczania prezentuje się następująco:
Na szczęście możemy zaoszczędzić sobie tych obliczeń i uzyskać wektory normalne naszej sfery w inny sposób.
Zauważmy, że wektor
Aby otrzymać wektor normalny w punkcie (2 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


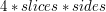 do
do 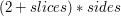 kosztem dodatkowej
tablicy o rozmiarze
kosztem dodatkowej
tablicy o rozmiarze 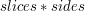 .
.
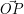 z Rys. 3. ma początek w środku układu
współrzędnych i koniec w punkcie
z Rys. 3. ma początek w środku układu
współrzędnych i koniec w punkcie  . Wektor
. Wektor 

