Runda 32 - Ptaki-dziwaki
07.06.2010 - Damian Rusak

Zawody Stałe, runda 32 Limit czasowy: 2s; Limit pamięciowy: 32 MB
Ptaki-dziwaki
Za głębię dalekiej dżungli na drugim końcu świata obrały swe leże tajemnicze ptaki-dziwaki. Ptaki te zawsze zamieszkują na rozłożystych drzewach. Matka Natura obdarzyła te piękne stworzenia barwnymi pióropuszami. Ptaki jednak mają problemy ze wzrokiem - nie tylko nie są w stanie dojrzeć barwy swego pióropusza, ale nie najlepiej idzie im też spoglądanie na inne okazy swego gatunku. Drzewo, które ptaki zamieszkują, składa się z dziupli, połączonych gałęziami. Każda gałąź łączy dokładnie dwie dziuple, żadne gałęzie nie przecinają się, z każdej dziupli można przejść do każdej innej na dokładnie jeden sposób po gałęziach, no bo to drzewo. Każda dziupla jest zamieszkana przez dokładnie jednego ptaka, każdy ma też dokładnie jedną siedzibę. Ptak-dziwak widzi tylko kolory pióropuszy swoich bezpośrednich sąsiadów (ptaków, do których dziupli może dojść po jednej gałęzi). Ptaki-dziwaki to bardzo dumny gatunek. Każdy ptak jest święcie przekonany, że jego pióropusz ma unikalną barwę. W tym złudzeniu utrzymuje ptaki fakt, że nie widzą koloru swego pióropusza. Jednak coś może zasiać ziarno niepokoju w ptasich sercach - gdyby któryś z nich zauważył, że pewne dwa sąsiadujące z nim ptaki mają pióropusze tego samego koloru, mógłby pomyśleć - "Ojej, może i mnie to dotyczy?!". Ptaki zatem unikają mieszkania w takiej okolicy. Na ich nieszczęście, Ty jako wytrwały badacz ptaków-dziwaków wiesz, że jest tylko Wejście: Pierwsza linia wejścia zawiera liczbę całkowitą Pierwsza linia zawiera liczbę całkowitą Wyjście: Wyjście powinno zawierać, dla każdego przypadku testowego, słowo TAK jeśli można rozmieścić w każdej dziupli ptaka-dziwaka, tak aby żaden ptak nie sąsiadował z dwoma ptakami o tym samym kolorze pióropusza. W przeciwnym razie należy wypisać NIE. Przykład: Wejście: 2 2 3 0 0 0 3 3 2 0 0 2 1 0 0 0 Wyjście: NIE TAK Wyjaśnienie:
Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto.
(2 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com



 różnych kolorów pióropuszy u tego gatunku. Przyglądasz się właśnie pięknemu drzewu i zastanawiasz się, czy mogłoby zostać "zaptaszone" przez ptaki-dziwaki, to jest czy ptaki o pewnych kolorach spośród
różnych kolorów pióropuszy u tego gatunku. Przyglądasz się właśnie pięknemu drzewu i zastanawiasz się, czy mogłoby zostać "zaptaszone" przez ptaki-dziwaki, to jest czy ptaki o pewnych kolorach spośród  (
(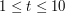 ), oznaczającą ilość przypadków testowych. Każdy przypadek testowy ma poniższą postać:
), oznaczającą ilość przypadków testowych. Każdy przypadek testowy ma poniższą postać: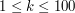 ), oznaczającą liczbę różnych kolorów pióropuszy u ptaków-dziwaków. W kolejnej linii jest podany opis drzewa w postaci rekurencyjnej - jeśli poniżej pewnej dziupli nie znajdują się już inne dziuple, jej opis to liczba
), oznaczającą liczbę różnych kolorów pióropuszy u ptaków-dziwaków. W kolejnej linii jest podany opis drzewa w postaci rekurencyjnej - jeśli poniżej pewnej dziupli nie znajdują się już inne dziuple, jej opis to liczba  . W przeciwnym razie opisem drzewa jest liczba
. W przeciwnym razie opisem drzewa jest liczba  - ilość dziupli poniżej połączonych gałęzią z obecnie rozpatrywaną dziuplą, po czym podane są kolejno opisy tych dziupli. (Spójrz dla jasności na przykład poniżej). Liczba dziupli w drzewie nie przekroczy
- ilość dziupli poniżej połączonych gałęzią z obecnie rozpatrywaną dziuplą, po czym podane są kolejno opisy tych dziupli. (Spójrz dla jasności na przykład poniżej). Liczba dziupli w drzewie nie przekroczy 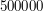 .
.