Runda 31 - Kolejna cegła w murze
24.05.2010 - Damian Rusak
 
Zawody stałe, runda 31. Limit czasowy: 3s; Limit pamięciowy: 32 MB
Kolejna cegła w murzePink nie lubi chodzić do szkoły. Woli włóczyć się po ulicach zamiast pilnie się uczyć. Ostatnio Pink zauważył, że niedaleko znajduje się wielki stary mur. Niektórych cegieł brakuje z powodu wandalizmu i upływu czasu - gdzieniegdzie wielkie dziury szpecą piękno muru. Pink zauważył, że w niektórych miejscach mur jest mniej stabilny niż w innych - dziury w murze osłabiają jego konstrukcję. Czysto teoretycznie zaczął zastanawiać się nad tym, którą cegłę można by wyjąć, tak aby jak najbardziej osłabić mur. Cegły w murze poukładane są w rzędach i Pink postanowił ocenić stabilność cegły przez to, jak wiele cegieł znajduje się ponad i pod daną cegłą. Nie zna się on za dobrze na fizyce, więc przyjął uproszczony model obliczeń - "nad" cegłą są trzy cegły w rzędzie powyżej (ta bezpośrednio nad oraz dwie sąsiadujące rogami), pięć cegieł w kolejnym rzędzie, siedem w trzecim ponad i tak dalej. Podobnie ze zliczaniem cegieł poniżej. Ponieważ zbliża się koncert rockowy, na którym bardzo Pinkowi zależy, nie ma czasu na znalezienie najbardziej stabilnej cegły. Pomóż mu i napisz program, który policzy, która z cegieł jest najbardziej stabilna.
(Na rysunku powyżej cegły zaznaczone na zielono są odpowiednio nad i pod czerwoną cegłą)
Wejście: Pierwsza linia wejścia zawiera dwie liczby całkowite Wyjście: Jedyna linia wyjścia powinna zawierać jedną liczbę całkowitą - największą stabilność pojedynczej cegły w murze (liczoną jako ilość cegieł nad i pod nią). Oczywiście stabilność posiadają jedynie istniejące cegły (pozycje z liczbą Przykład: Wejście: 4 6 1 1 0 0 0 0 1 1 0 0 1 1 1 0 0 0 1 1 1 0 1 1 0 0 Wyjście: 6 Np. cegła na drugiej pozycji w drugim rzędzie ma nad sobą dwie, a pod sobą cztery cegły.
Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto.
(3 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com




 i
i  - (
- (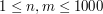 ), odpowiednio wysokość i szerokość muru. W kolejnych
), odpowiednio wysokość i szerokość muru. W kolejnych  , jeśli na danej pozycji znajduje się cegła, albo
, jeśli na danej pozycji znajduje się cegła, albo  , jeśli na tej pozycji jest dziura w murze. Mur niekoniecznie musi być zgodny z logiką (tj. mogą pojawić się w nim "wiszące w powietrzu" cegły).
, jeśli na tej pozycji jest dziura w murze. Mur niekoniecznie musi być zgodny z logiką (tj. mogą pojawić się w nim "wiszące w powietrzu" cegły).

