Runda 29 - Jabłkomachia
10.05.2010 - Damian Rusak

Zawody stałe, runda 29. Limit czasowy: 1s; Limit pamięciowy: 32MB
Jabłkomachia
Robak Jim nie ma łatwego życia. Nie tylko nie poszczęściło mu się z miejscem urodzenia - mieszka w wielkim sześciennym jabłku, ale też zdrowie psychiczne Jima pozostawia wiele do życzenia. W jego wnętrzu ścierają się ze sobą dwie siły - Zdrowy Rozsądek i Wielki Głód (w skrócie Zer i Wieg). Zer i Wieg dawno już porzucili swoje szczytne ideały i obecnie ich jedynym celem i rozrywką jest wzajemna walka. Oczywiście chcą wykorzystać w tym celu Jima. Oto szczegóły ich podłej gry: Siedziba Jima to nieskończonej wielkości jabłko w kształcie sześcianu. Jim ma bardzo specyficzny sposób poruszania się po jabłku - można sobie wyobrazić, że jabłko jest podzielone na jednostkowe sześcianiki o krawędziach równoległych do krawędzi jabłka. Zer i Wieg przypisali każdemu sześcianikowi trzy liczby - współrzędne kartezjańskie (uznajemy, że sześcianik w dolnym narożniku jabłka ma współrzędne Jim jest bardzo zmieszany całą tą sytuacją i poprosił Cię o pomoc. Chciałby, abyś napisał mu program, który, znając początkową pozycję Jima, odpowie mu na pytanie, który z jego wewnętrznych demonów zwycięży. Wejście: Pierwsza linia wejścia zawiera liczbę całkowitą Wyjście: Dla każdego przypadku testowego należy wypisać w nowej linii słowo "TAK", jeśli Zer, rozpoczynając, jest zawsze w stanie wygrać, niezależnie od ruchów Wiega, bądź "NIE" w przeciwnym przypadku. Przykład: Wejście: 2 2 2 0 1 1 1 Wyjście: NIE TAK
Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto.
(1 ocena) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com



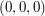 ). Całe jabłko zajmuje obszar przestrzeni, zawierający sześcianiki o współrzędnych nieujemnych. Jim zajmuje dokładnie jeden sześcianik i zawsze znajduje się w całości wewnątrz jednego sześcianika. Zer i Wieg na zmianę przejmują kontrolę nad Jimem i każą mu przejść do pewnego sześcianika, sąsiadującego z obecnym miejscem położenia Jima. Jeśli Jim znajduje się w sześcianiku
). Całe jabłko zajmuje obszar przestrzeni, zawierający sześcianiki o współrzędnych nieujemnych. Jim zajmuje dokładnie jeden sześcianik i zawsze znajduje się w całości wewnątrz jednego sześcianika. Zer i Wieg na zmianę przejmują kontrolę nad Jimem i każą mu przejść do pewnego sześcianika, sąsiadującego z obecnym miejscem położenia Jima. Jeśli Jim znajduje się w sześcianiku 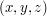 , może przejść (o ile nie wykroczy poza jabłko, tj. dopóki współrzędne są nieujemne) do sześcianków
, może przejść (o ile nie wykroczy poza jabłko, tj. dopóki współrzędne są nieujemne) do sześcianków  ,
,  ,
,  lub
lub  . Gracz wygrywa, gdy po jego ruchu Jimem, Jim znajdzie się w sześcianiku
. Gracz wygrywa, gdy po jego ruchu Jimem, Jim znajdzie się w sześcianiku  , (
, (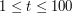 ), oznaczającą liczbę przypadków testowych. W kolejnych
), oznaczającą liczbę przypadków testowych. W kolejnych  ,
, ,
, , (
, ( ) oznaczające współrzędne początkowego ustawienia Jima.
) oznaczające współrzędne początkowego ustawienia Jima. 

