Runda 28 - Trudna podróż
03.05.2010 - Damian Rusak
 
Zawody Stałe, runda 28. Limit czasowy: 3s; Limit pamięciowy: 64MB Trudna podróż
Jak co roku, gdy rozkwita wiosna, Andrzej wyciągnął ze swojego garażu starego malucha. Marzy mu się podróż do dalekiej miejscowości uzdrowiskowej, gdzie będzie mógł wreszcie zrelaksować się po miesiącach spędzonych przed komputerem i odpocząć trochę od pizzy na telefon i wysokich rachunków za internet. Do owej miejscowości można dostać się korzystając z sieci lokalnych dróg. Drogi przejeżdżają przez wiele miast i miasteczek, w tym też przez miejsce zamieszkania Andrzeja oraz przez uzdrowisko. Każda droga jest dwukierunkowa i łączy dokładnie dwa miasta. Drogi nie przecinają się, ale mogą biec poprzez tunele i estakady. Andrzej oszacował już, ile minut zajmie mu pokonanie każdej z dróg i zanotował sobie to na mapie podróżnej. Niestety, to nie jedyna przeszkoda, jaka czeka na Andrzeja - jego samochód nie jest w najlepszym stanie. W związku z tym, po przejechaniu każdej drogi potrzebuje kilku małych napraw. Po pierwszej przejechanej drodze zajmie to Andrzejowi minutę, ale po drugiej już dwie minuty, potem trzy i tak dalej - po każdym przejechanym mieście koszt naprawy wzrasta o jeden (wliczając w to naprawę po przyjeździe do uzdrowiska). Biorąc pod uwagę tę małą niedogodność, pomóż Andrzejowi wybrać drogę, która najprędzej zaprowadzi go do uzdrowiska. Wejście: Pierwsza linia wejścia zawiera dwie liczby całkowite Wyjście: Na wyjście wypisz jedną liczbę całkowitą - najmniejszą liczbę minut, jaką może trwać podróż Andrzeja.
Przykład 1: wejście: 4 4 1 2 1 2 3 1 3 4 1 1 4 7 wyjście: 8 Wyjaśnienie: droga poprzez miasta 1,2,3,4 ma co prawda długość 3, lecz kolejne naprawy kosztują 1+2+3, co w sumie daje 9. Droga bezpośrednio z 1 do 4 kosztuje 7 oraz 1 za naprawę - łącznie 8.
Przykład 2: wejście: 5 5 1 2 1 2 3 1 3 5 1 1 4 3 4 5 4 wyjście: 9
Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto.
|
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com



 i
i  (
(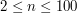 ,
, 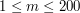 ), oznaczających kolejno liczbę miast i łączących je dróg. Miasta numerowane są od
), oznaczających kolejno liczbę miast i łączących je dróg. Miasta numerowane są od  do
do 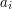
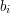 oraz
oraz 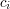 - oznaczające drogę z miasta
- oznaczające drogę z miasta 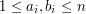 ,
, 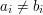 ,
, 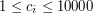 ).
).

