Zawody stałe, runda 23
Limit czasowy: 2s; Limit pamięciowy: 32MB
Wybuchowa Owca
Góry Bajtocji pełne są porośniętych bujną i pyszną trawą polan, na których pasą się owieczki. Łączą je ze sobą długie, kręte i jałowe wąwozy.
Słynący z nieprzeciętnej (jak na owcę) inteligencji Alfred wiódłby wśród nich spokojne i beztroskie życie, gdyby nie codzienny strach przed byciem zjedzonym. O tak - tłuściutkie Bajtockie owieczki przyciągnęły do okolicy naturalnego wroga - wilki. Walka z nimi wydaje się co najmniej nierówna. Wilk jest nie tylko szybszy od owcy - dysponuje on świetnym węchem, intuicją i skończył z wyróżnieniem wilczy kurs psychologii ofiary. Innymi słowy - ma lata doświadczeń w zjadaniu kolegów Alfreda i doskonale wie co takiej owcy chodzi po głowie.
Dlatego Alfred, jak każda szanujące swoje życie owca, zawsze nosi przy sobie kilka lasek dynamitu - wystarczająco dużo by jeden jedyny raz, kiedy znajduje się bezpiecznie na jakiejś polanie, móc wysadzić dokładnie jeden z wąwozów do niej prowadzących, blokując tym samym przejście. O ile oczywiście wilk nie będzie już na niej czekał, lub nie przybędzie na nią w tej samej chwili...
O wilku mowa! Ten właśnie się przebudził i postanowił zjeść porządne śniadanie. Znajdujący się w niebezpieczeństwie Alfred zna położenie wilczego legowiska oraz przeciętną prędkość wilka, jednak nie potrafi przewidzieć jego ruchów. Oboje za to dysponują dokładną mapą okolicy. Jakim wynikiem zakończy się polowanie - czy wilk będzie syty, czy owca będzie cała?
Wejście:
W pierwszej linii wejścia znajdują się dwie liczby całkowite 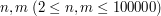 - kolejno ilość hal, oraz ilość wąwozów.
- kolejno ilość hal, oraz ilość wąwozów.
W drugiej linii wejścia dwie liczby - numery hal na których znajdują się wilk oraz Alfred.
W trzeciej linii wejścia znajdują się dwie liczby całkowite 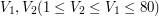 - ilość metrów jakie pokonują kolejno wilk oraz Alfred w ciągu każdej sekundy.
- ilość metrów jakie pokonują kolejno wilk oraz Alfred w ciągu każdej sekundy.
Czas potrzeby na pokonanie hali jest pomijalny.
W dalszych  liniach znajdują się opisy wąwozów postaci
liniach znajdują się opisy wąwozów postaci 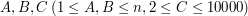 - oznacza to że polany
- oznacza to że polany  oraz
oraz  łączy wąwóz długości
łączy wąwóz długości  metrów.
metrów.
Każde dwie polany łączy co najwyżej jeden wąwóz, żadne dwa wąwozy się nie przecinają.
Wyjście:
Napis "NIE" jeśli Alfred nie ma szans w walce z wilkiem. W przeciwnym wypadku minimalną ilość czasu (zaokrągloną w górę do pełnych sekund), po której Alfred będzie mógł spokojnie skupić się na skubaniu trawy.
Przykład 1:
Dane:
5 5
1 5
5 3
1 2 5
2 3 5
3 4 8
4 5 4
5 3 5
Wynik:
2
Przykład 2:
Dane:
5 5
1 3
4 3
1 2 4
2 3 6
3 4 3
4 5 5
4 1 5
Wynik:
NIE
Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany.
Zaloguj się lub
załóż konto.





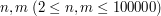 - kolejno ilość hal, oraz ilość wąwozów.
- kolejno ilość hal, oraz ilość wąwozów.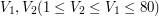 - ilość metrów jakie pokonują kolejno wilk oraz Alfred w ciągu każdej sekundy.
- ilość metrów jakie pokonują kolejno wilk oraz Alfred w ciągu każdej sekundy. liniach znajdują się opisy wąwozów postaci
liniach znajdują się opisy wąwozów postaci 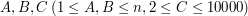 - oznacza to że polany
- oznacza to że polany  oraz
oraz  łączy wąwóz długości
łączy wąwóz długości  metrów.
metrów.

