K - Knowledge for the masses
08.01.2010
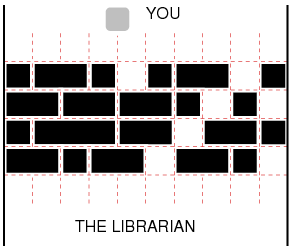
    Time limit: 30 s You are in a library equipped with bookracks that move on rails. There are many parallel rails, i.e., the bookracks are organized in several rows, see figure:
To borrow a book, you have to find the librarian, who seems to hide on the opposite side of the bookracks.
Your task then is to move the racks along the rails so that a passage forms.
Each rack has a certain integer width, and can be safely positioned at any integer point along the rail.
(A rack does not block in a non-integer position and could accidentally move in either direction).
The racks in a single row need not be contiguous — there can be arbitrary (though integer) space between two successive bookracks.
A passage is formed at position
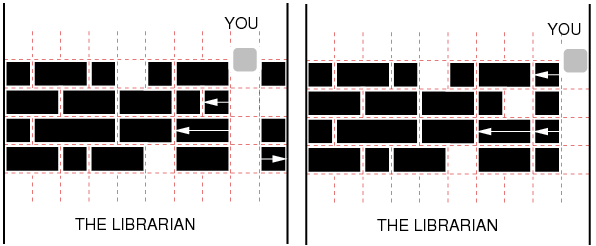
Moving a rack requires a certain amount of effort on your part: moving it in either direction costs 1. This cost does not depend on the distance of the shift, which can be explained by a well known fact that static friction is considerably higher than kinetic friction. Still, you are here to borrow a book, not to work out, so you would like to form a passage (at any position) with as little effort as possible. Multiple Test Cases
The input contains several test cases. The first line of the input contains a positive integer Single Instance Input
Two space separated integers Single Instance OutputIn the first line, your program should output the minimum cost of making a passage through the bookracks. In the second line, it should print out the increasing sequence of all the positions at which a minimum cost passage can be formed. ExampleInput1 4 10 8 1 2 1 0 1 2 0 1 7 2 2 2 1 0 1 0 6 1 3 2 0 2 1 7 2 1 2 0 2 1 0 Output3 8 9 Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto. |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


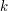 if there is no bookrack in the interval
if there is no bookrack in the interval 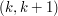 in any row
(somehow you don't like the idea of trying to find a more sophisticated passage in this maze.)
in any row
(somehow you don't like the idea of trying to find a more sophisticated passage in this maze.)
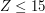 ,
denoting the number of test cases. Then
,
denoting the number of test cases. Then 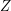 test cases follow, each conforming to the format described in
section Single Instance Input. For each test case, your program has to write an output conforming
to the format described in section Single Instance Output.
test cases follow, each conforming to the format described in
section Single Instance Input. For each test case, your program has to write an output conforming
to the format described in section Single Instance Output.
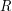 and
and 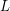 (
(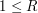 ,
, 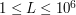 )
are given in the first line of an input instance.
They denote the number of rows and the width of each and every row, respectively.
Then
)
are given in the first line of an input instance.
They denote the number of rows and the width of each and every row, respectively.
Then 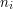 ,
followed by
,
followed by 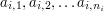 , all separated by single spaces.
Number
, all separated by single spaces.
Number 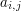 denotes either the width of a bookrack when
denotes either the width of a bookrack when 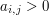 or a unit of empty space when
or a unit of empty space when 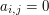 .
Note that for any row
.
Note that for any row 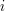 ,
, 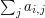 equals
equals
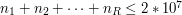 . Moreover, there will be
at least one
. Moreover, there will be
at least one 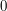 in the description of each row, which means that creating a passage is always possible.
in the description of each row, which means that creating a passage is always possible.


