Time limit: 25 s
Memory limit: 64 MB
Deep in the Carribean, there is an island even stranger than the Monkey Island,
dwelled by Horatio Torquemada Marley.
Not only it has a rectangular shape, but is also divided into an 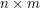 grid. Each grid field has a certain height.
Unfortunately, the sea level started to raise and in year
grid. Each grid field has a certain height.
Unfortunately, the sea level started to raise and in year 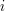 , the level is
, the level is 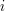 meters.
Another strange feature of the island is that it is made of sponge, and the water can freely
flow through it.
Thus, a grid field whose height is at most the current sea level is considered flooded.
Adjacent unflooded fields (i.e., sharing common edge) create unflooded areas.
Sailors are interested in the number of unflooded areas in a given year.
meters.
Another strange feature of the island is that it is made of sponge, and the water can freely
flow through it.
Thus, a grid field whose height is at most the current sea level is considered flooded.
Adjacent unflooded fields (i.e., sharing common edge) create unflooded areas.
Sailors are interested in the number of unflooded areas in a given year.
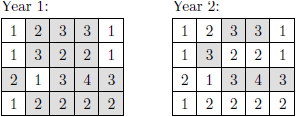
An example of a 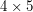 island is given below. Numbers denote the heights of
respective fields in meters.
Unflooded fields are darker; there are two unflooded areas in the first year
and three areas in the second year.
island is given below. Numbers denote the heights of
respective fields in meters.
Unflooded fields are darker; there are two unflooded areas in the first year
and three areas in the second year.
Multiple Test Cases
The input contains several test cases. The first line of the input contains a positive integer 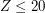 ,
denoting the number of test cases. Then
,
denoting the number of test cases. Then 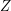 test cases follow, each conforming to the format described in
section Single Instance Input. For each test case, your program has to write an output conforming
to the format described in section Single Instance Output.
test cases follow, each conforming to the format described in
section Single Instance Input. For each test case, your program has to write an output conforming
to the format described in section Single Instance Output.
Single Instance Input
The first line contains two numbers  and
and 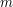 separated by a single space, the dimensions of
the island, where
separated by a single space, the dimensions of
the island, where 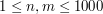 .
Next
.
Next  lines contain
lines contain 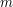 integers from the range
integers from the range ![$ [1,10^9] $](/files/tex/6172f3df744e488418b5be751ea5ebd0c503c86a.png) separated by single spaces, denoting the heights of the respective fields.
Next line contains an integer
separated by single spaces, denoting the heights of the respective fields.
Next line contains an integer 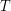 (
(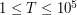 ). The last line
contains
). The last line
contains 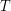 integers
integers 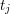 , separated by single spaces, such that
, separated by single spaces, such that
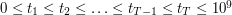 .
.
Single Instance Output
Your program should output a single
line consisting of 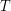 numbers
numbers 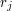 separated by single spaces,
where
separated by single spaces,
where 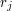 is the number of unflooded areas in year
is the number of unflooded areas in year 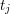 .
.
Example
Input
1
4 5
1 2 3 3 1
1 3 2 2 1
2 1 3 4 3
1 2 2 2 2
5
1 2 3 4 5
Output
2 3 1 0 0
Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany.
Zaloguj się lub
załóż konto.





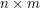 grid. Each grid field has a certain height.
Unfortunately, the sea level started to raise and in year
grid. Each grid field has a certain height.
Unfortunately, the sea level started to raise and in year 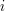 , the level is
, the level is 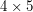 island is given below. Numbers denote the heights of
respective fields in meters.
Unflooded fields are darker; there are two unflooded areas in the first year
and three areas in the second year.
island is given below. Numbers denote the heights of
respective fields in meters.
Unflooded fields are darker; there are two unflooded areas in the first year
and three areas in the second year.

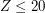 ,
denoting the number of test cases. Then
,
denoting the number of test cases. Then 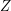 test cases follow, each conforming to the format described in
section Single Instance Input. For each test case, your program has to write an output conforming
to the format described in section Single Instance Output.
test cases follow, each conforming to the format described in
section Single Instance Input. For each test case, your program has to write an output conforming
to the format described in section Single Instance Output.
 and
and 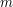 separated by a single space, the dimensions of
the island, where
separated by a single space, the dimensions of
the island, where 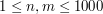 .
Next
.
Next ![$ [1,10^9] $](/files/tex/6172f3df744e488418b5be751ea5ebd0c503c86a.png) separated by single spaces, denoting the heights of the respective fields.
Next line contains an integer
separated by single spaces, denoting the heights of the respective fields.
Next line contains an integer 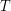 (
(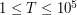 ). The last line
contains
). The last line
contains 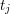 , separated by single spaces, such that
, separated by single spaces, such that
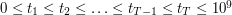 .
.
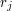 separated by single spaces,
where
separated by single spaces,
where 

