C - Cave
08.01.2010
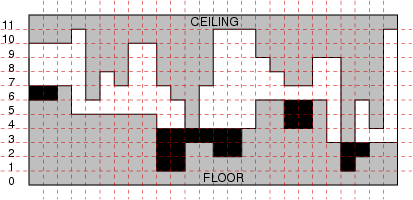
   Time limit: 16 s As an owner of a land with a cave you were delighted when you last heard that underground fuel tanks are great business. Of course, the more volume one can store, the better. In case of your cave, the effective volume is not easy to calculate, because the cave has a rather sophisticated shape (see figure). Thank heavens it is degenerate in one dimension!
Furthermore, there is some electrical wiring on the ceiling of the cave. You can never be sure if the insulation is intact, so you want to keep the fuel level just below the ceiling at every point. You can pump the fuel to whatever spots in the cave you choose, possibly creating several ponds. Bear in mind though that the fuel is a liquid, so it minimises its gravitational energy, e.g., it will run evenly in every direction on a flat horizontal surface, pour down whenever possible, obey the rule of communicating vessels, etc. As the cave is degenerate and you can make the space between the fuel level and the ceiling arbitrarily small, you actually want to calculate the maximum possible area of ponds that satisfy aforementioned rules. Multiple Test Cases
The input contains several test cases. The first line of the input contains a positive integer Single Instance Input
In the first line of an input instance, there is
an integer Single Instance OutputYour program is to print out one integer: the maximum total area of admissible ponds in the cave. ExampleInput1 15 6 6 7 5 5 5 5 5 5 1 1 3 3 2 2 10 10 10 11 6 8 7 10 10 7 6 4 7 11 11 Output14 Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto. |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


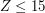 ,
denoting the number of test cases. Then
,
denoting the number of test cases. Then 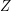 test cases follow, each conforming to the format described in
section Single Instance Input. For each test case, your program has to write an output conforming
to the format described in section Single Instance Output.
test cases follow, each conforming to the format described in
section Single Instance Input. For each test case, your program has to write an output conforming
to the format described in section Single Instance Output.
 (
(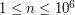 ) denoting the width of the cave.
The second line of input consists of
) denoting the width of the cave.
The second line of input consists of 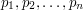 and
the third line consists of
and
the third line consists of 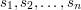 , separated by single spaces.
The numbers
, separated by single spaces.
The numbers 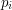 and
and 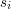 satisfy
satisfy 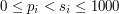 and denote the floor and
ceiling level at interval
and denote the floor and
ceiling level at interval 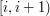 , respectively.
, respectively.


