Multiplikatywna odwrotność a modulo n
Mamy daną liczbę  . Bardzo przydatną umiejętnością będzie dla nas znajdowanie takiej liczby
. Bardzo przydatną umiejętnością będzie dla nas znajdowanie takiej liczby  , że
, że  przemnożone przez
przemnożone przez  da nam
da nam 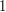 . Oczywiście modulo
. Oczywiście modulo  . Analogicznie do liczb rzeczywistych, taką liczbę będziemy nazywali odwrotnością liczby
. Analogicznie do liczb rzeczywistych, taką liczbę będziemy nazywali odwrotnością liczby  i zapisywać będziemy jako
i zapisywać będziemy jako 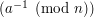 . Formalnie:
. Formalnie:
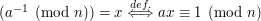
Jeśli  jest względnie pierwsze z
jest względnie pierwsze z  to
to  ma dokładnie jedną odwrotność modulo
ma dokładnie jedną odwrotność modulo  . W przeciwnym przypadku nie ma odwrotności.
. W przeciwnym przypadku nie ma odwrotności.
Odwrotnością liczby 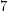 modulo
modulo 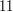 jest liczba
jest liczba 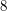 bo
bo 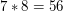 , a
, a 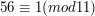 . Odwrotnością liczby
. Odwrotnością liczby  modulo
modulo 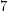 jest liczba
jest liczba 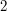 bo
bo 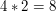 , a
, a 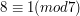 . Natomiast odwrotność liczby
. Natomiast odwrotność liczby 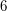 modulo
modulo 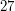 nie istnieje, bo
nie istnieje, bo 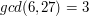 .
.
Rodzi się naturalne pytanie jak szybko znajdować taką odwrotność. Z pomocą przychodzi nam rozszerzony algorytm Euklidesa (o rozszerzonym algorytmie Euklidesa możesz poczytać w artykule znajdującym się tutaj):
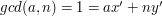
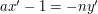
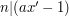
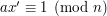
Zatem, aby obliczyć odwrotność, wystarczy uruchomić rozszerzony algorytm Euklidesa dla argumentów  oraz
oraz  . Jest to bardzo dobra wiadomość, bo i tak musielibyśmy odpalić ten algorytm, aby sprawdzić czy odwrotność w ogóle istnieje.
. Jest to bardzo dobra wiadomość, bo i tak musielibyśmy odpalić ten algorytm, aby sprawdzić czy odwrotność w ogóle istnieje.
Rozwiązała nam się zagadka z tym kiedy możemy obustronnie podzielić równanie przez jakąś liczbę 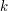 . Powiedziałem w poprzednim rozdziale, że możemy to zrobić gdy
. Powiedziałem w poprzednim rozdziale, że możemy to zrobić gdy 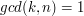 . Nie wiemy jeszcze tylko dlaczego właśnie wtedy. Chwileczkę! Przecież wiemy! Skoro
. Nie wiemy jeszcze tylko dlaczego właśnie wtedy. Chwileczkę! Przecież wiemy! Skoro 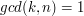 to
to 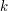 ma multiplikatywną odwrotność modulo
ma multiplikatywną odwrotność modulo  . Liczba ta jest liczbą całkowitą - więc możemy przez nią obustronnie pomnożyć równanie. Formalnie zapisując:
. Liczba ta jest liczbą całkowitą - więc możemy przez nią obustronnie pomnożyć równanie. Formalnie zapisując:
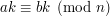
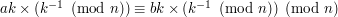
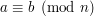
Jeśli namieszaliśmy trochę za bardzo to wszystko powinien wyjaśnić przykład. Mamy równanie 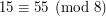 . Chcemy podzielić obustronnie przez
. Chcemy podzielić obustronnie przez 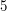 . Wiemy, że odwrotnością liczby 5 modulo 8 jest 5 bo
. Wiemy, że odwrotnością liczby 5 modulo 8 jest 5 bo 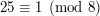 . Zatem mnożymy przez odwrotność piątki obie strony równania i otrzymujemy
. Zatem mnożymy przez odwrotność piątki obie strony równania i otrzymujemy 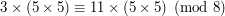 . Ponieważ
. Ponieważ 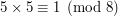 otrzymujemy
otrzymujemy 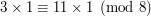 czyli
czyli 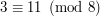 . Podzieliliśmy obie strony przez 5. Ponadto zrobiliśmy to bez żadnego błędu - co można łatwo sprawdzić.
. Podzieliliśmy obie strony przez 5. Ponadto zrobiliśmy to bez żadnego błędu - co można łatwo sprawdzić.
Poznaliśmy zatem jedno zastosowanie multiplikatywnej odwrotności modulo. W kolejnych działach poznamy dwa kolejne. A tymczasem czy drogi Czytelnik potrafi podać przykład jakiejś liczby która nie ma odwrotności modulo 143? I czy potrafisz uzasadnić czemu jeśli istnieje jakaś odwrotność danej liczby, to jest ona jedyna?
Własność podzielności liczb
Pewnie większość z was wie, że liczba N jest podzielna przez 3 wtedy i tylko wtedy gdy suma cyfr tej liczby jest podzielna przez 3. Na przykład 17265 jest podzielna przez 3 bo 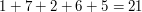 a 21 jest podzielne przez 3. Ale czy wiecie dlaczego tak jest? Właśnie teraz ten dowód przeprowadzimy. Weźmy dowolną liczbę N i zapiszmy ją w systemie dziesiętnym:
a 21 jest podzielne przez 3. Ale czy wiecie dlaczego tak jest? Właśnie teraz ten dowód przeprowadzimy. Weźmy dowolną liczbę N i zapiszmy ją w systemie dziesiętnym: 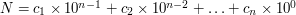 . Określmy wielomian wzorem
. Określmy wielomian wzorem 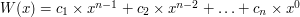 . Naturalnie
. Naturalnie 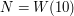 . Ponadto skorzystamy z prostego faktu, że
. Ponadto skorzystamy z prostego faktu, że 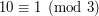 . Z własności wielomianów o którym mówiliśmy w drugim rozdziale wiemy już że:
. Z własności wielomianów o którym mówiliśmy w drugim rozdziale wiemy już że:
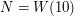
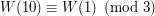
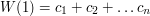
Zatem 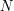 jest podzielna przez
jest podzielna przez 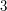 wtedy i tylko wtedy gdy suma jej cyfr jest podzielna przez
wtedy i tylko wtedy gdy suma jej cyfr jest podzielna przez 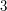 !
!
Spróbujmy teraz znaleźć regułę na podzielność przez 13. Tym razem liczbę N podzielimy na blocki po 3 liczby: 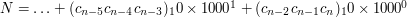 oraz
oraz 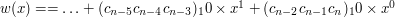 . Tym razem skorzystamy z tego, że
. Tym razem skorzystamy z tego, że 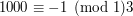 (bo
(bo 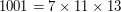 ). Zatem liczba N dzieli się przez 7 wtedy i tylko wtedy gdy suma naprzemienna:
). Zatem liczba N dzieli się przez 7 wtedy i tylko wtedy gdy suma naprzemienna: 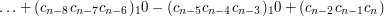 dzieli się przez 7. Ponieważ jak wspomnieliśmy
dzieli się przez 7. Ponieważ jak wspomnieliśmy 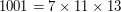 reguła ta odnosi się również do podzielności przez 11 oraz 7.
reguła ta odnosi się również do podzielności przez 11 oraz 7.
Umiemy już odpowiedzieć na pierwsze nasze pytanie. 13 dzieli 16971461287794 bo 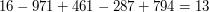 . Jako ćwiczenie sprawdź czy liczba
. Jako ćwiczenie sprawdź czy liczba 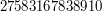 jest podzielna przez
jest podzielna przez 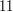 .
.




 . Bardzo przydatną umiejętnością będzie dla nas znajdowanie takiej liczby
. Bardzo przydatną umiejętnością będzie dla nas znajdowanie takiej liczby  , że
, że 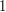 . Oczywiście modulo
. Oczywiście modulo  . Analogicznie do liczb rzeczywistych, taką liczbę będziemy nazywali odwrotnością liczby
. Analogicznie do liczb rzeczywistych, taką liczbę będziemy nazywali odwrotnością liczby 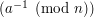 . Formalnie:
. Formalnie: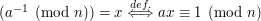
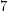 modulo
modulo 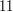 jest liczba
jest liczba 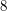 bo
bo 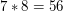 , a
, a 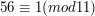 . Odwrotnością liczby
. Odwrotnością liczby  modulo
modulo 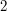 bo
bo 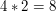 , a
, a 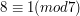 . Natomiast odwrotność liczby
. Natomiast odwrotność liczby 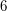 modulo
modulo 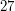 nie istnieje, bo
nie istnieje, bo 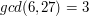 .
.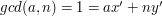
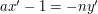
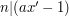
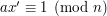
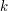 . Powiedziałem w poprzednim rozdziale, że możemy to zrobić gdy
. Powiedziałem w poprzednim rozdziale, że możemy to zrobić gdy 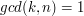 . Nie wiemy jeszcze tylko dlaczego właśnie wtedy. Chwileczkę! Przecież wiemy! Skoro
. Nie wiemy jeszcze tylko dlaczego właśnie wtedy. Chwileczkę! Przecież wiemy! Skoro 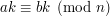
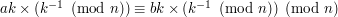
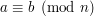
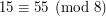 . Chcemy podzielić obustronnie przez
. Chcemy podzielić obustronnie przez 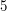 . Wiemy, że odwrotnością liczby 5 modulo 8 jest 5 bo
. Wiemy, że odwrotnością liczby 5 modulo 8 jest 5 bo 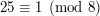 . Zatem mnożymy przez odwrotność piątki obie strony równania i otrzymujemy
. Zatem mnożymy przez odwrotność piątki obie strony równania i otrzymujemy 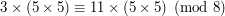 . Ponieważ
. Ponieważ 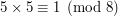 otrzymujemy
otrzymujemy 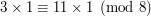 czyli
czyli 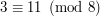 . Podzieliliśmy obie strony przez 5. Ponadto zrobiliśmy to bez żadnego błędu - co można łatwo sprawdzić.
. Podzieliliśmy obie strony przez 5. Ponadto zrobiliśmy to bez żadnego błędu - co można łatwo sprawdzić.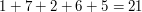 a 21 jest podzielne przez 3. Ale czy wiecie dlaczego tak jest? Właśnie teraz ten dowód przeprowadzimy. Weźmy dowolną liczbę N i zapiszmy ją w systemie dziesiętnym:
a 21 jest podzielne przez 3. Ale czy wiecie dlaczego tak jest? Właśnie teraz ten dowód przeprowadzimy. Weźmy dowolną liczbę N i zapiszmy ją w systemie dziesiętnym: 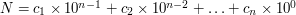 . Określmy wielomian wzorem
. Określmy wielomian wzorem 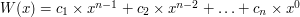 . Naturalnie
. Naturalnie 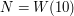 . Ponadto skorzystamy z prostego faktu, że
. Ponadto skorzystamy z prostego faktu, że 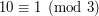 . Z własności wielomianów o którym mówiliśmy w drugim rozdziale wiemy już że:
. Z własności wielomianów o którym mówiliśmy w drugim rozdziale wiemy już że: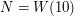
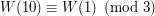
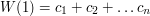
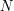 jest podzielna przez
jest podzielna przez 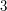 wtedy i tylko wtedy gdy suma jej cyfr jest podzielna przez
wtedy i tylko wtedy gdy suma jej cyfr jest podzielna przez 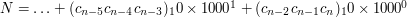 oraz
oraz 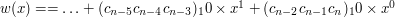 . Tym razem skorzystamy z tego, że
. Tym razem skorzystamy z tego, że 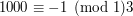 (bo
(bo 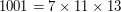 ). Zatem liczba N dzieli się przez 7 wtedy i tylko wtedy gdy suma naprzemienna:
). Zatem liczba N dzieli się przez 7 wtedy i tylko wtedy gdy suma naprzemienna: 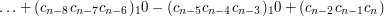 dzieli się przez 7. Ponieważ jak wspomnieliśmy
dzieli się przez 7. Ponieważ jak wspomnieliśmy 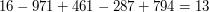 . Jako ćwiczenie sprawdź czy liczba
. Jako ćwiczenie sprawdź czy liczba 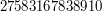 jest podzielna przez
jest podzielna przez 

