Biorytmy
Limit czasowy: 3s; Limit pamięciowy: 32MB;
Uniwersyteckie Zawody Informatyczne 2003
Niektórzy ludzie wierzą, że w życiu człowieka występują trzy cykle, które rozpoczynają się w dniu narodzin. Te trzy cykle to fizyczny, emocjonalny i intelektualny. Mają one długości odpowiednio 23, 28 i 33 dni. W każdym okresie każdego cyklu występuje punkt kulminacyjny. W punkcie kulminacyjnym osoba prezentuje się najlepiej odpowiednio fizycznie, emocjonalnie lub intelektualnie. Przykładowo jeśli weźmiemy krzywą intelektualną, to procesy myślowe są bardziej klarowne, a koncentracja łatwiejsza.
Poniważ trzy cykle mają różną długość okresu, to ich punkty kulminacji generalnie występują w różnych momentach. Chcemy obliczyć kiedy występuje potrójny punkt kulminacyjny (gdy wszystkie trzy cykle mają punkt kulminacyjny tego samego dnia) dla danej osoby. Dla każdego cyklu masz daną liczbę dni od początku danego rok do wystąpienia punktu kulminacji (niekoniecznie pierwszego w danym roku). Masz daną również datę w roku jako liczbę dni od początku roku. Twoim zadaniem jest wyznaczenie liczby dni od podanej daty do następnego potrójnego punktu kulminacji. Podany dzień nie jest liczony. Przykładowo jeśli dany jest dzień 10 a potrójny punkt kulminacji występuje dnia 12, to odpowiedź brzmi 2, a nie 3. Jeśli potrójny punkt kulminacji występuje w podanym dniu, to powinieneś podać liczbę dni do następnego jego wystąpienia.
Wejście
Na wejściu wystąpi pewna liczba zestawów danych. Dla każdego zestawu w pojedyńczej linii podane są cztery liczby całkowite f, e, i oraz d. Liczby f, e oraz i są liczbami dni od początku roku bieżącego w których występują odpowiednio fizyczny, emocjonalny i intelektualny punkt kulminacji. Wartość d wyznacza podaną datę i może być mniejsza od którejkolwiek z liczb f, e lub i. Wszystkie liczby są nieujemne i conajwyżej równe 365. Możesz założyć, że potrójny punkt kulminacji wystąpi w ciągu 21252 dni od podanego dnia. Koniec wejścia jest oznaczony poprzez linię 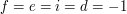 .
.
Wyjście
Dla każdego zestawu danych wypisz numer zestawu oraz odpowiedź zawierającą informacje o liczbie dni do następnego wystąpienia potrójnego punktu kulminacji w formie:
Case 1: the next triple peak occurs in 1234 days.
Użyj liczby mnogiej ``days'' nawet jeśli odpowiedzią jest 1.
Przykład
Dla danych wejściowych:
0 0 0 0
0 0 0 100
5 20 34 325
4 5 6 7
283 102 23 320
203 301 203 40
-1 -1 -1 -1
Poprawną odpowiedzią jest:
Case 1: the next triple peak occurs in 21252 days.
Case 2: the next triple peak occurs in 21152 days.
Case 3: the next triple peak occurs in 19575 days.
Case 4: the next triple peak occurs in 16994 days.
Case 5: the next triple peak occurs in 8910 days.
Case 6: the next triple peak occurs in 10789 days.
Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany.
Zaloguj się lub
załóż konto.
Klikowce
Limit czasowy: 20s; Limit pamięciowy: 32MB;
Potyczki Algorytmiczne 2008
Graf nieskierowany nazywamy klikowcem, jeśli każda jego spójna składowa jest kliką. Maurycy narysował sobie na kartce wszystkie n-wierzchołkowe klikowce i ma zamiar ocenić piękno każdego z nich liczbą ze zbioru 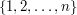 (różne klikowce mogą otrzymać równe oceny). Na ile sposobów może to zrobić? Wynik należy podać modulo 1
(różne klikowce mogą otrzymać równe oceny). Na ile sposobów może to zrobić? Wynik należy podać modulo 1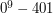 . Na poniższym rysunku przedstawiono wszystkie klikowce dla n = 3.
. Na poniższym rysunku przedstawiono wszystkie klikowce dla n = 3.
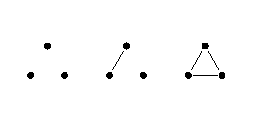
Wejście
W jedynym wierszu standardowego wejścia znajdują się dwie liczby całkowite n oraz m (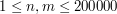 ), oddzielone pojedynczym odstępem i oznaczające odpowiednio liczbę wierzchołków każdego klikowca i liczbę ocen.
), oddzielone pojedynczym odstępem i oznaczające odpowiednio liczbę wierzchołków każdego klikowca i liczbę ocen.
Wyjście
W jedynym wierszu standardowego wyjścia należy wypisać liczbę możliwych zestawów ocen modulo 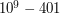 .
.
Przykład
Dla danych wejściowych
3 2
Poprawną odpowiedzią jest
8
Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany.
Zaloguj się lub
załóż konto.




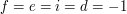 .
.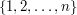 (różne klikowce mogą otrzymać równe oceny). Na ile sposobów może to zrobić? Wynik należy podać modulo 1
(różne klikowce mogą otrzymać równe oceny). Na ile sposobów może to zrobić? Wynik należy podać modulo 1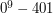 . Na poniższym rysunku przedstawiono wszystkie klikowce dla n = 3.
. Na poniższym rysunku przedstawiono wszystkie klikowce dla n = 3.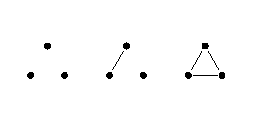
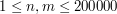 ), oddzielone pojedynczym odstępem i oznaczające odpowiednio liczbę wierzchołków każdego klikowca i liczbę ocen.
), oddzielone pojedynczym odstępem i oznaczające odpowiednio liczbę wierzchołków każdego klikowca i liczbę ocen.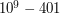 .
.

