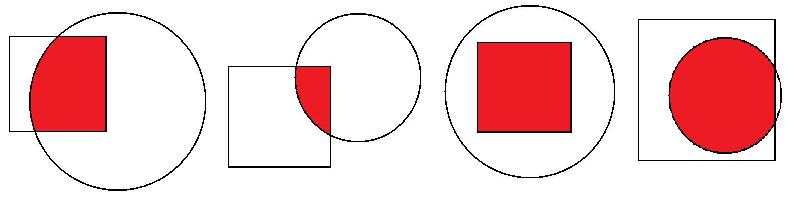
Runda 14 - Kwadrat i koło
04.01.2010 - Damian Rusak
  
Zawody stałe, runda 14. Limit czasowy: 1s; Limit pamięciowy: 32MB; Kwadrat i koło
Rolnik Joe posiada kwadratowe pole, na którym uprawia buraki. Pewnego dnia do jego drzwi zapukali przedstawiciele władz i oznajmili mu, że w pobliżu jego ziem rząd planuje zbudować kopalnię. Wobec tego chcą odkupić od Joe'go fragment jego pola. Kopalnia i przyległe tereny zajmują obszar o kształcie koła o środku w lokalizacji kopalni. Rząd planuje zapłacić Joemu dolara za każdy Zadanie: Mając daną długość boku kwadratowego pola Joe'go (przyjmujemy, że jego lewy dolny róg znajduje się w punkcie (0,0) a jego boki są równoległe do osi układu współrzędnych), współrzędne środka koła wytyczanego przez tereny kopalniane i jego promień, odpowiedz na pytanie, ile rząd zapłaci Joe'mu. Wejście: Pierwsza linia wejścia zawieta liczbę Wyjście: Dla każdego przypadku testowego na wyjściu powinna pojawić się w nowej linii jedna liczba rzeczywista z dokładnością do 3 miejsc po przecinku - liczba dolarów, jaką zapłacą Joe'mu przedstawiciele władz. Przykład: Wejście: 2 6 3 3 3 6 10 20 3 Wyjście: 28.274 0.000
Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto.
(2 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com



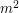 zajętej ziemi. Znając rozmiary swojego pola, lokalizację kopalni, oraz promień koła terenów kopalnianych, Joe chciałby dowiedzieć się, ile otrzyma pieniędzy. Rząd chce od niego kupić jedynie teren wspólny dla pola Joego i planowanego obszaru kopali.
zajętej ziemi. Znając rozmiary swojego pola, lokalizację kopalni, oraz promień koła terenów kopalnianych, Joe chciałby dowiedzieć się, ile otrzyma pieniędzy. Rząd chce od niego kupić jedynie teren wspólny dla pola Joego i planowanego obszaru kopali. - ilość przypadków testowych.
- ilość przypadków testowych. 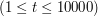 . Kolejno następują opisy zestawów danych. Dla każdego zestawu danych jedna linia zawiera cztery liczby rzeczywiste -
. Kolejno następują opisy zestawów danych. Dla każdego zestawu danych jedna linia zawiera cztery liczby rzeczywiste - 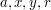 ,
, 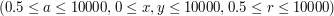 - oznaczające kolejno długość boku kwadratu, współrzędne środka koła, oraz jego promień, w metrach.
- oznaczające kolejno długość boku kwadratu, współrzędne środka koła, oraz jego promień, w metrach.