Zawody stałe, runda 12;
Limit czasowy: 3s; Limit pamięciowy: 128MB;
W pewnym sadzie rośnie krzak. Na owym krzaku mieszka rodzina biedronek. Każda biedronka umiłowała sobie jedno miejsce krzaka i tam ustanowiła swoją siedzibę. Krzak składa się z liści i gałęzi. Jest tak wielki, że nawet najstarsze biedronki nie wiedzą, jak jest wielki. Wiedzą za to, że każdy liść krzaka jest połączony za pomocą gałęzi z dokładnie dwoma liśćmi powyżej. Wiedzą też, że pierwszy liść rośnie tuż przy ziemi, oraz że z każdego liścia można dojść do każdego innego (przechodząc po gałązkach i innych liściach) na dokładnie jeden sposób. Aby ułatwić sobie życie, biedronki ponumerowały liście - ten najniższy ma numer 1 oraz każde dwa liście, z którymi jest połączony niżej położony liść o numerze  mają numery
mają numery 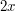 i
i 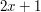 . Rodzina biedronek wpadła na pomysł, aby poodwiedzać się nawzajem. Każdego dnia jedna z biedronek udaje się w odwiedziny do drugiej, idąc tylko po liściach i gałęziach, po czym wraca do swojego domku. Tak dla każdej pary biedronek - kiedyś pierwsza odwiedzi drugą, a innym razem druga pierwszą. Mówimy, że biedronka przeszła w podróży
. Rodzina biedronek wpadła na pomysł, aby poodwiedzać się nawzajem. Każdego dnia jedna z biedronek udaje się w odwiedziny do drugiej, idąc tylko po liściach i gałęziach, po czym wraca do swojego domku. Tak dla każdej pary biedronek - kiedyś pierwsza odwiedzi drugą, a innym razem druga pierwszą. Mówimy, że biedronka przeszła w podróży  gałęzi, jeśli po drodze do innej i z powrotem przeszła łącznie po
gałęzi, jeśli po drodze do innej i z powrotem przeszła łącznie po  gałęziach. Rodzina zastanawia się, ile łącznie przyjdzie im przejść gałęzi, przy założeniu, że każda biedronka wyprawi się do każdej innej dokładnie raz.
gałęziach. Rodzina zastanawia się, ile łącznie przyjdzie im przejść gałęzi, przy założeniu, że każda biedronka wyprawi się do każdej innej dokładnie raz.
Zadanie:
Mając zadaną ilość biedronek w rodzinie oraz numery siedzib biedronek na krzaku, oblicz, ile w sumie przejdą biedronki, jeśli każda z nich wyruszy do każdej innej. (po każdej podróży biedronka wraca do swojego liścia).
Wejście:
Pierwsza linia wejścia zawiera jedną liczbę naturalną 
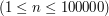 - oznaczającą ilość biedronek w rodzinie. W kolejnym wierszu znajduje się
- oznaczającą ilość biedronek w rodzinie. W kolejnym wierszu znajduje się  liczb
liczb 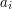 oznaczających numer siedziby
oznaczających numer siedziby  -tej biedronki
-tej biedronki 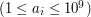 . Może się zdarzyć, że kilka biedronek mieszka w tym samym miejscu - wtedy koszt odwiedzenia się tych par wynosi zero.
. Może się zdarzyć, że kilka biedronek mieszka w tym samym miejscu - wtedy koszt odwiedzenia się tych par wynosi zero.
Wyjście:
Wyjście powinno się składać z jednej linii, zawierającej jedną liczbę - ilość gałązek, które w sumie przebędą biedronki, jeśli każda odwiedzi każdą inną. Możesz założyć, że odpowiedź nie przekroczy 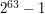 .
.
Przykład:
Wejście:
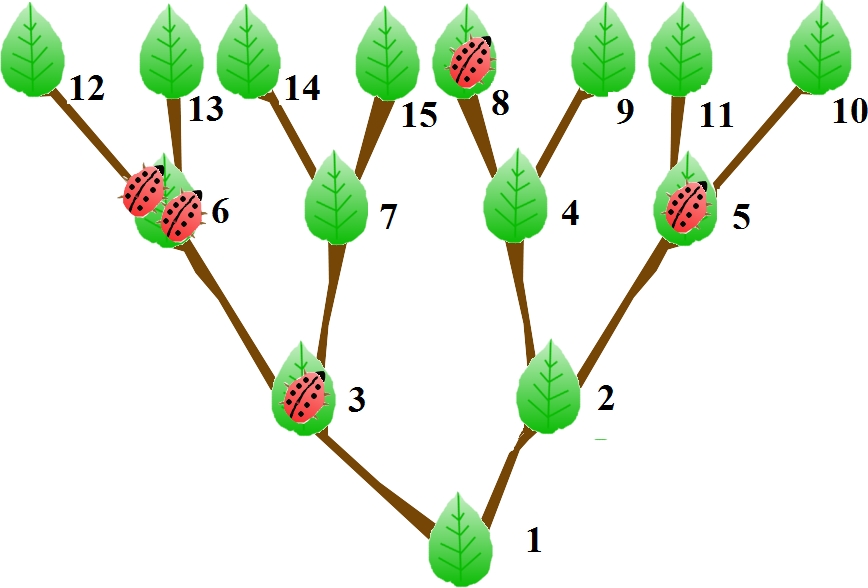
5
3 6 5 8 6
Wyjście:
120
Biedronka z 3 liścia: 2*(1 + 1 + 3 + 4) -> 18
Biedronki z 6 liścia - każda po 2 * (1 + 4 + 5) -> 40
Biedronka z 8 liścia 2*(5 + 5 + 3 + 4) -> 34
Biedronka z 5 liścia 2*(3 + 3 + 4 + 4) -> 28
Łącznie 120
Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany.
Zaloguj się lub
załóż konto.





 mają numery
mają numery 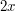 i
i 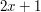 . Rodzina biedronek wpadła na pomysł, aby poodwiedzać się nawzajem. Każdego dnia jedna z biedronek udaje się w odwiedziny do drugiej, idąc tylko po liściach i gałęziach, po czym wraca do swojego domku. Tak dla każdej pary biedronek - kiedyś pierwsza odwiedzi drugą, a innym razem druga pierwszą. Mówimy, że biedronka przeszła w podróży
. Rodzina biedronek wpadła na pomysł, aby poodwiedzać się nawzajem. Każdego dnia jedna z biedronek udaje się w odwiedziny do drugiej, idąc tylko po liściach i gałęziach, po czym wraca do swojego domku. Tak dla każdej pary biedronek - kiedyś pierwsza odwiedzi drugą, a innym razem druga pierwszą. Mówimy, że biedronka przeszła w podróży  gałęzi, jeśli po drodze do innej i z powrotem przeszła łącznie po
gałęzi, jeśli po drodze do innej i z powrotem przeszła łącznie po 
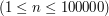 - oznaczającą ilość biedronek w rodzinie. W kolejnym wierszu znajduje się
- oznaczającą ilość biedronek w rodzinie. W kolejnym wierszu znajduje się 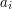 oznaczających numer siedziby
oznaczających numer siedziby  -tej biedronki
-tej biedronki 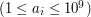 . Może się zdarzyć, że kilka biedronek mieszka w tym samym miejscu - wtedy koszt odwiedzenia się tych par wynosi zero.
. Może się zdarzyć, że kilka biedronek mieszka w tym samym miejscu - wtedy koszt odwiedzenia się tych par wynosi zero.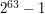 .
.


