Zawody stałe, runda 9.
Limit czasowy: 15s; Limit pamięciowy: 64 MB;
Trzy Wieże
Król Pewnej Krainy posiada w swym kraju trzy wspaniałe wieże. Jedna jest koloru czerwonego, jedna zielonego, a jeszcze jedna mieni się osobliwym odcieniem błękitu. Cały kraj podzielony jest na powiaty, w modnym stylu kwadratowym - z lotu ptaka wygląda jak prostokąt, złożony z identycznych kwadratowych pól. Na trzech z nich stoją piękne wieże. Król postanowił, że musi stale kontrolować sytuację w państwie, wydał więc rozkaz zbudowania dróg w królewstwie, tak aby mógł podróżować pomiędzy swymi siedzibami. W każdym powiecie król może zbudować drogi - mówimy wtedy, że powiat jest przejezdny. Z wieży można przedostać się do dowolnego powiatu przejezdnego, który sąsiaduje z nią z południa, wschodu, północy lub zachodu. Podobnie król jest w stanie przeprawić się z jednego przejezdnego powiatu do każdego innego, zlokalizowanego tuż za jedną z czterech granic. Oczywiście król jest bardzo skąpy i zażądał, aby jego nadworny informatyk znalazł taki plan zagospodarowania powiatów, aby z każdej wieży można się było przedostać do dwóch pozostałych, i aby jak najmniej powiatów zostało uczynionych przejezdnymi. Pojawił się jednak problem - niektóre powiaty są położone na bardzo trudnym terenie i król nie chce marnować pieniędzy na prowadzenie przez nie dróg. Zatem wytyczone trasy nie mogą przebiegać przez te wyklęte tereny.
Zadanie:
Mając dany plan królewstwa, oblicz, ile co najmniej powiatów trzeba uczynić przejezdnymi, aby możliwe było przebycie pomiędzy każdymi dwoma wieżami, tak, że wybieramy jedynie powiaty, które nie są położone na trudnym terenie.
Wejście:
Pierwsza linia wejścia zawiera liczbę 
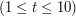 - oznaczającą ilość przypadków testowych. Kolejno następuje
- oznaczającą ilość przypadków testowych. Kolejno następuje  zestawów danych. Każdy zestaw wygląda następująco: W pierwszej linii dwie liczby -
zestawów danych. Każdy zestaw wygląda następująco: W pierwszej linii dwie liczby -  i
i 
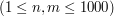 , oznaczające wysokość i szerokość planu królewstwa. W kolejnych
, oznaczające wysokość i szerokość planu królewstwa. W kolejnych  liniach znajduje się po
liniach znajduje się po  znaków, oznaczających kolejne powiaty na kolejnych wysokościach planu. Znak '_' oznacza powiat, po którym można podróżować. Znak 'X' oznacza powiat położony na trudnym terenie. Na wejściu pojawią się też trzy litery - 'A', 'B', 'C' - oznaczające położenie trzech wież. Możesz założyć, że żadne dwie wieże nie są położone bezpośrednio w swoim sąsiedztwie (tj. nie sąsiadują ze sobą na północ, południe, wschód ani zachód). Powiaty, w których znajdują się wieże, możesz uznać za przejezdne. Po każdym zestawie danych następuje pusta linia.
znaków, oznaczających kolejne powiaty na kolejnych wysokościach planu. Znak '_' oznacza powiat, po którym można podróżować. Znak 'X' oznacza powiat położony na trudnym terenie. Na wejściu pojawią się też trzy litery - 'A', 'B', 'C' - oznaczające położenie trzech wież. Możesz założyć, że żadne dwie wieże nie są położone bezpośrednio w swoim sąsiedztwie (tj. nie sąsiadują ze sobą na północ, południe, wschód ani zachód). Powiaty, w których znajdują się wieże, możesz uznać za przejezdne. Po każdym zestawie danych następuje pusta linia.
Wyjście:
Dla każdego zestawu danych należy wypisać jedną linię zawierającą słowo "NIE", jeśli nie jest możliwe połączenie wież (np. trudny teren skutecznie odgradza wieże od siebie), bądź w przeciwynym przypadku jedną liczbę - najmniejszą liczbę powiatów, które należy uczynić przejezdnymi, aby możliwa była podróż między każdą parą wież.
Przykład:
Wejście:
2
6 9
_______XX
_X___X___
_XA___X__
_XX__B___
__X______
________C
6 9
____X__B_
_C_______
____X_XX_
X_X___X__
__X_A____
_________
Wyjście:
7
9
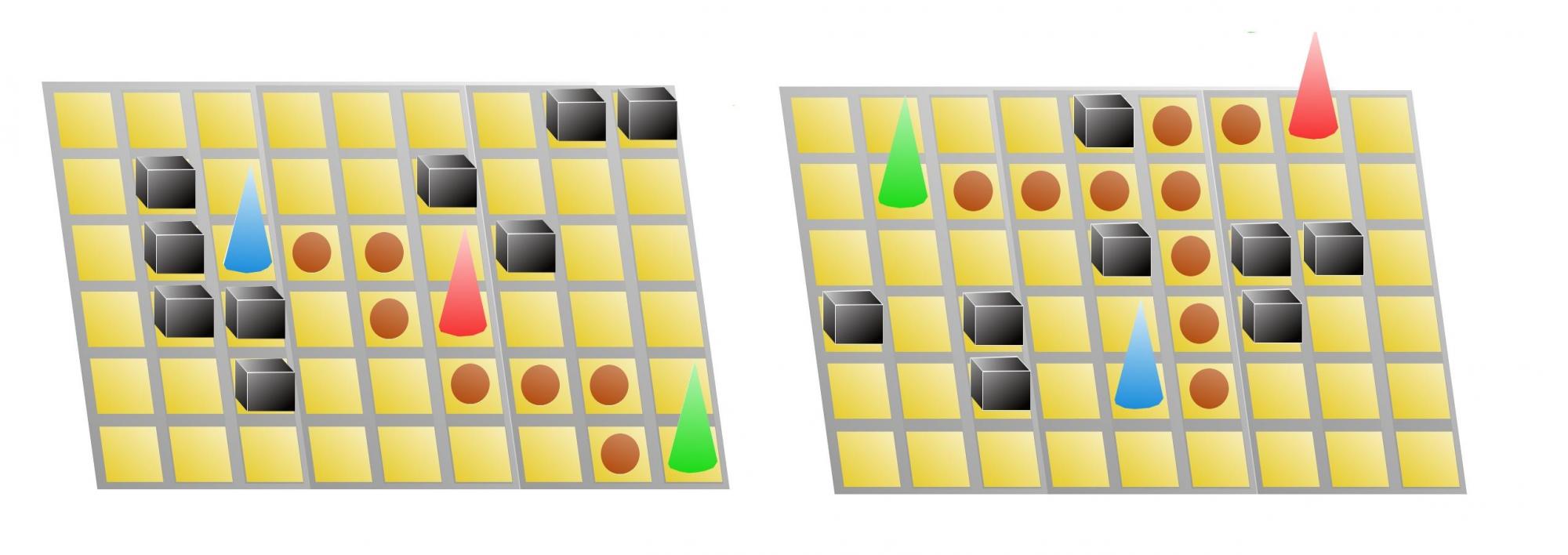
Przykład 1: Najmniej powiatów zostanie uczynionych przyjezdnymi, gdy wybierzemy powiaty zaznaczone brązowymi kołami.
Przykład 2: W tym przykładzie nie opłaca się łaczyć wież "po kolei" - można wybrać mniej powiatów (jak na rysunku).
Zapraszamy do dyskusji na temat zadania na forum.
Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany.
Zaloguj się lub
załóż konto.






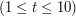 - oznaczającą ilość przypadków testowych. Kolejno następuje
- oznaczającą ilość przypadków testowych. Kolejno następuje  i
i 
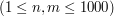 , oznaczające wysokość i szerokość planu królewstwa. W kolejnych
, oznaczające wysokość i szerokość planu królewstwa. W kolejnych 


