Zawody stałe, runda 6
Limit czasowy 2s; Limit pamięciowy 32MB
Plusy i Minusy
Cały świat oszlał na punkcie plusów i minusów! Ludzie na ulicy wciąż rozmawiają o plusach i minusach, tematyka dodawania i odejmowania opanowała telewizję, gazety i radio. Trochę dziwna moda, ale co możemy z tym zrobić? Najlepiej podporządkować się trendom i polubić proste działania. Oczywiście informatycy wolą rzeczy trochę ambitniejsze i zawsze muszą wymyślić sobie ciekawszy problem. Miasta i wsie pogrążają się w oparach plusominusowego absurdu, ale na horyzoncie pojawiło się światełko nadziei - interesujący problem!
Mamy dany ciąg liczb naturalnych. Pomiędzy każdymi dwoma kolejnymi możemy wstawić plus albo minus. Możemy też otoczyć dowolny blok liczb nawiasami. Wykonujemy działania zgodnie z ich normalną kolejnością, np:
(5 + 3) - (6 - 3) = 8 - 3 = 5
(5 + 3 - 6) - 3 = 2 - 3 = -1
Słyszałeś, że ktoś w popularnym programie telewizyjnym zadaje gościom pytania o takie ciągi - czy da się w ciągu liczb tak poustawiać plusy, minusy i nawiasy, aby otrzymać dany wynik? Napisz program, który zaszokuje wszystkich i odpowie szybko i sprawnie na takie pytanie!
Zadanie:
Napisz program, który dla danego ciągu liczb naturalnych i pewnej liczby zapytań, odpowie dla każdego zapytania, czy można otrzymać podaną sumę z tego ciągu, poprzez nawiasowanie i ustawienie plusów i minusów pomiędzy liczbami. Znak minus może stać przed pierwszą liczbą.
Wejście:
W pierwszej linii wejścia znajdują się dwie liczby naturalne 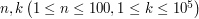 , oznaczające kolejno ilość liczb w ciągu i ilość zapytań. W kolejnej linii znajduje się
, oznaczające kolejno ilość liczb w ciągu i ilość zapytań. W kolejnej linii znajduje się  liczb naturalnych
liczb naturalnych 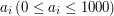 . W kolejnych
. W kolejnych  liniach znajdują się liczby
liniach znajdują się liczby 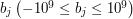 , oznaczające kolejne zapytania.
, oznaczające kolejne zapytania.
Wyjście:
Wyjście powinno składać się z  linii, po jednej dla każdego zapytania. W j-tej linii powinno się znaleźć słowo TAK , jeśli liczbę
linii, po jednej dla każdego zapytania. W j-tej linii powinno się znaleźć słowo TAK , jeśli liczbę 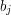 można otrzymać jako wynik dodawań i odejmowań ponawiasowanych elementów ciągu
można otrzymać jako wynik dodawań i odejmowań ponawiasowanych elementów ciągu 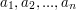 .
.
Przykład:
Wejście:
4 4
1 2 3 4
10
-7
0
-10
Wyjście:
TAK
NIE
TAK
TAK
1) 1 + 2 + 3 + 4 = 10
2) -7 nie da się uzyskać w ten sposób
3) - 1 + (2 + 3) - 4 = 0
4) - (1 + 2 + 3 + 4) = -10
Zapraszamy do dyskusji na temat zadania na forum.
Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany.
Zaloguj się lub
załóż konto.





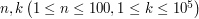 , oznaczające kolejno ilość liczb w ciągu i ilość zapytań. W kolejnej linii znajduje się
, oznaczające kolejno ilość liczb w ciągu i ilość zapytań. W kolejnej linii znajduje się  liczb naturalnych
liczb naturalnych 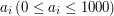 . W kolejnych
. W kolejnych  liniach znajdują się liczby
liniach znajdują się liczby 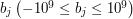 , oznaczające kolejne zapytania.
, oznaczające kolejne zapytania.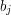 można otrzymać jako wynik dodawań i odejmowań ponawiasowanych elementów ciągu
można otrzymać jako wynik dodawań i odejmowań ponawiasowanych elementów ciągu 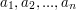 .
.

