Chińska komórka
03.10.2009 - Paweł Gawrychowski
  Nie jest to może moje ulubione zadanie (nie wygrałem dzięki jego rozwiązaniu żadnych zawodów :), ale na pewno jest bardzo fajnym przykładem użycia dość ogólnej techniki, którą warto znać. Także dlatego, że w dość zaskakujący sposób pojawia się w niej geometria obliczeniowa (mam nadzieję, że nie zniechęci to Was to dalszej lektury...), mimo że zadanie na pierwszy (a nawet na drugi) rzut oka nie ma nic wspólnego z geometrią. Ale po kolei... Zadanie
Treść można zobaczyć na przykład tutaj. Po przedarciu się przez historyjkę problem wygląda następująco: dostajemy ciąg Pierwszy pomysł
..jest dość oczywisty: możemy użyć programowania dynamicznego. Niech
![$ S[a,b]=f_a+2f_{a+1}+3f_{a+2}+\ldots+(b-a+1)f_b $](/files/tex/7c40797cbe868fbc18539206e818be304ef07bba.png) . Musimy jednak poradzić sobie z dwoma problemami: . Musimy jednak poradzić sobie z dwoma problemami:
Drugi pomysł, trochę lepszy
Skoro wyznaczenie pojedynczej wartości
![$ b_j=f(j)-B[j]-jA[j] $](/files/tex/d53d69c2a968af8acc4d42f5230ba694d86bc8a5.png) , , ![$ a_j=A[j] $](/files/tex/951b948c7da4ec23147358b719b475d92021f2a7.png) oraz oraz 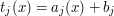 widać, że tak naprawdę interesuje nas wyznaczenie widać, że tak naprawdę interesuje nas wyznaczenie 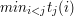 dla wszystkich wartości dla wszystkich wartości 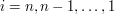 . W tym momencie możemy całkiem zapomnieć o pierwotnym sformułowaniu problem i zająć się tylko i wyłącznie wyznaczaniem takich minimów z funkcji liniowych (no, prawie: przydatne będzie jeszcze to, że współczynniki . W tym momencie możemy całkiem zapomnieć o pierwotnym sformułowaniu problem i zająć się tylko i wyłącznie wyznaczaniem takich minimów z funkcji liniowych (no, prawie: przydatne będzie jeszcze to, że współczynniki 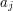 są wszystkie dodatnie i coraz większe dla kolejnych wartości są wszystkie dodatnie i coraz większe dla kolejnych wartości  ). ).
Jak minimalizować funkcje liniowe?
Popatrzmy przez chwilę na prostszą wersję problemu: dla danego zbioru funkcji liniowych 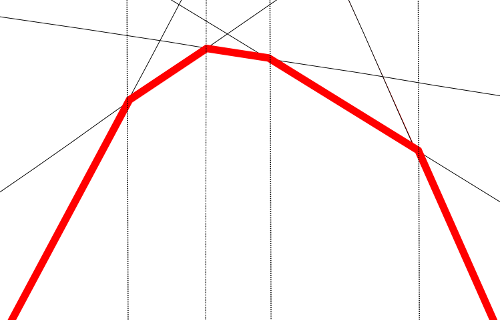
Krzywą zaznaczoną na czerwono będziemy nazywali górną otoczką funkcji
No dobrze, ale w naszym problemie zbiór funkcji liniowych nie był podany z góry: dla kolejnych wartości 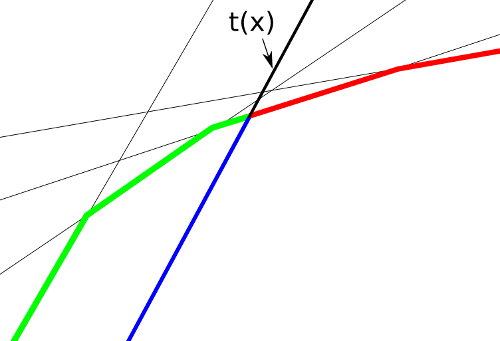
w powyższej sytuacji trzeba zastąpić zielony fragment przedziałem, na którym optymalna jest niebieski fragment nowej funkcji. Jeżeli kolejno dodawane funkcje mają coraz większe współczynniki przy
Zastanówmy się chwilę nad kosztem takiej aktualizacji. Może się zdarzyć, że dodanie nowej funkcji spowoduje konieczność usunięcia wielu odcinków, jednak powoduje utworzenie tylko jednego nowego. Z drugiej strony ciężko usunąć coś czego nie ma, a więc (wszystkich) usunięć nie będzie więcej niż
Oprócz aktualizacji musimy jednak również znaleźć przedział, w którym znajduje się bieżąca wartość Cała implementacja nie jest bardzo skomplikowana, o ile umiemy wyliczać przecięcia dwóch odcinków/prostych. Tego typu "prymitywy" geometryczne (jak przecięcie, sprawdzanie po której stronie prostej leży punkt, liczenie odległości od prostej, znajdowanie okręgu przechodzącego przez dane punkty, itd) warto:
Czy to już koniec?
W zasadzie tak: umiemy już wyznaczyć optymalny koszt. Autor zadania prosi nas też o wyznaczenie najlepszego podziału (a nawet jest bardziej wybredny i wymaga, żeby był on najmniejszy leksykograficznie), jednak podany wyżej pomysł można łatwo wzbogacić o znajdowanie nie tylko najmniejszego kosztu, ale także funkcji, dla której jest on osiągany. Cały algorytm będzie miał złożoność Co jeszcze?Co prawda nie ma to żadnego związku z minimalizacją funkcji liniowych, ale wszystkim, którym podobało się użycie otoczki do rozwiązania problemu, który wydawał się nie mieć nic wspólnego z geometrią, polecam następujące zadanie:
Mamy dane trzy substancje chemiczne A,B i C (Czytelnik może zastąpić litery swoimi ulubionymi pierwiastkami). Dysponujemy oraz zastanowienie się nad warunkami, które musi spełniać funkcja kosztu, aby znajdowanie optymalnego podziału na fragmenty można było przyspieszyć tak, jak w przypadku zadaniu o komórce. (4 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com



 liczb
liczb 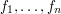 , mamy pokroić go na
, mamy pokroić go na  kawałków
kawałków 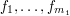 ,
, 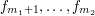 , ...,
, ..., 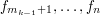 tak, aby zminimalizować sumę ich kosztów. Kosztem fragmentu
tak, aby zminimalizować sumę ich kosztów. Kosztem fragmentu 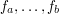 nazywamy
nazywamy 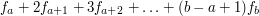 . Autor zadania prosi o podanie zarówno tej minimalnej sumy, jak i optymalnego podziału, jednak my zajmiemy się tylko wyznaczeniem najmniejszego możliwego kosztu.
. Autor zadania prosi o podanie zarówno tej minimalnej sumy, jak i optymalnego podziału, jednak my zajmiemy się tylko wyznaczeniem najmniejszego możliwego kosztu.
![$ T[i,j] $](/files/tex/0a5c2be101cf7e522837cc2182b3c223bde8c633.png) oznacza koszt pokrojenia sufiksu
oznacza koszt pokrojenia sufiksu 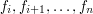 na
na 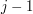 kawałków. Czyli wszystkie
kawałków. Czyli wszystkie ![$$ T[n+1,0] = 0$$](/files/tex/7e32f9b5c7eb6b3d0eb51b2cd8a89600aaa8f931.png)
![$$ T[i,j] = \min_{i < s} T[s,j-1]+ S[i,s-1] $$](/files/tex/2c1407e475b7daa5bbfddd360cf114072cabb9ef.png)
![$ S[a,b] $](/files/tex/4828b29da9c1292c3d7e4095510e96978f2aaf4d.png) . Nie jest to bardzo trudne jeśli wcześniej wyliczymy (w czasie
. Nie jest to bardzo trudne jeśli wcześniej wyliczymy (w czasie 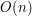 ) wartości
) wartości ![$ A[i]=f_i+f_{i+1}+\ldots +f_n $](/files/tex/36cf064efe859b52e535a61026fd7d7857027d7e.png) oraz
oraz ![$ B[i]=f_i+2f_{i+1}+\ldots + (n-i+1)f_n $](/files/tex/c037c6d02ffa93ae48dd77f8513204921cb493b7.png) korzystając z tego, że:
korzystając z tego, że:
![$$A[n+1]=B[n+1]=0$$](/files/tex/dbe10019dfaa2303b7c645b47ca416122c184616.png)
![$$A[i]=f_i+A[i+1]$$](/files/tex/d45b9dd5c72a9ab2d8b832ccdaa5cdd0deafac1d.png)
![$$B[i]=A[i]+B[i+1]$$](/files/tex/cf25478242c592ca7aebc6a2f60952d0c07217e3.png)
![$ S[a,b]=B[a]-B[b+1]-(b-a+1)A[b+1] $](/files/tex/6229073259f7e6c0c9784c1c28b44d0f39d80152.png) .
.
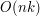 wartości
wartości 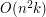 . W oryginalnej wersji
. W oryginalnej wersji ![$ f(i)=T[i,j] $](/files/tex/9c43557860bf426147d6b542db0aca89d8798cc4.png) dla ustalonego
dla ustalonego ![$ g(i)=T[i,j+1] $](/files/tex/0b8fcdb734e175238764206a80d91c83fe203878.png) . Co tak naprawdę musimy wyznaczyć?
. Co tak naprawdę musimy wyznaczyć?
![$$g(i)= min_{i < j} f(j) + S[i,j-1]$$](/files/tex/603e2396d8e25e1990cb530d46656cb34e8840cc.png)
![$$= min_{i < j} f(j) + B[i]-B[j]-(j-i)A[j]$$](/files/tex/8ef09c634994ff30d1ae781f1f51605483c463cf.png)
![$$= B[i] + min_{i<j} f(j) - B[j] - jA[j] + iA[j]$$](/files/tex/2c9bdc0d197f562fca9a6528e2ec0abc14e3a7dc.png)
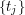 chcemy wyznaczać
chcemy wyznaczać 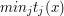 dla różnych wartości
dla różnych wartości  . Najlepiej nie przeglądając za każdym razem wszystkich funkcji... Rozwiązanie takiego problemu najłatwiej wyobrazić sobie na rysunku:
. Najlepiej nie przeglądając za każdym razem wszystkich funkcji... Rozwiązanie takiego problemu najłatwiej wyobrazić sobie na rysunku:
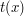 :
:
 , zastępowany fragment będzie zawsze prefiksem aktualnej otoczki (czyli rysunek wcale nie był tak tendencyjny, jak mogłoby się wydawać). Znacząco ułatwia to implementację aktualizacji, o ile przechowujemy opis aktualnej otoczki na stosie tak, aby odcinek najbardziej na lewo był na szczycie. Po dodaniu nowej funkcji wystarczy wtedy zdejmować ze szczytu stosu odcinki tak długo, jak znajdują się na lewo od nowej prostej. W momencie, gdy napotkamy odcinek, który ją przecina, trzeba "skrócić" go do punktu przecięcia.
, zastępowany fragment będzie zawsze prefiksem aktualnej otoczki (czyli rysunek wcale nie był tak tendencyjny, jak mogłoby się wydawać). Znacząco ułatwia to implementację aktualizacji, o ile przechowujemy opis aktualnej otoczki na stosie tak, aby odcinek najbardziej na lewo był na szczycie. Po dodaniu nowej funkcji wystarczy wtedy zdejmować ze szczytu stosu odcinki tak długo, jak znajdują się na lewo od nowej prostej. W momencie, gdy napotkamy odcinek, który ją przecina, trzeba "skrócić" go do punktu przecięcia.
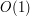 .
.
 . Użycie wyszukiwania binarnego dałoby nam złożoność
. Użycie wyszukiwania binarnego dałoby nam złożoność 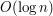 , co wydaje się trochę kiepskie, skoro mamy aktualizację w czasie stałym. Ale przecież tak naprawdę wcale nie potrzebujemy tego wyszukiwania binarnego! Szukamy coraz mniejszych wartości
, co wydaje się trochę kiepskie, skoro mamy aktualizację w czasie stałym. Ale przecież tak naprawdę wcale nie potrzebujemy tego wyszukiwania binarnego! Szukamy coraz mniejszych wartości 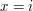 , na pewno już nam się nie przyda, możemy się więc go pozbyć. Czyli zamiast na stosie, otoczkę powinniśmy przechowywać w strukturze, która pozwala na dodawanie i usuwanie elementów z obydwu końców. Może to być lista dwukierunkowa lub (dla programujących w C++)
, na pewno już nam się nie przyda, możemy się więc go pozbyć. Czyli zamiast na stosie, otoczkę powinniśmy przechowywać w strukturze, która pozwala na dodawanie i usuwanie elementów z obydwu końców. Może to być lista dwukierunkowa lub (dla programujących w C++) 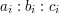 . Chcielibyśmy zmieszać (niektóre, być może wszystkie) je tak, aby otrzymać roztwór o proporcjach
. Chcielibyśmy zmieszać (niektóre, być może wszystkie) je tak, aby otrzymać roztwór o proporcjach 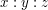 . Czy jest to możliwe?
. Czy jest to możliwe?


