Maski bitowe
03.10.2009 - Damian Rusak
   Pomocna w rozwiązaniu wielu problemów algorytmicznych z gatunku programowania dynamicznego bywa umiejętność zwięzłego zapisu wszystkich możliwych do osiągnięcia stanów. Spotykamy problemy, w których te stany to pewne podzbiory. Co to oznacza? W jaki sposób reprezentować podzbiory i czy faktycznie jest to dobry i skuteczny sposób rozwiązywania problemów algorytmicznych? Odpowiedzi na te pytania znajdziesz w tym artykule.
Problem KomiwojażeraZa przykład wykorzystania tej idei posłużyć nam może znany Problem Komiwojażera (TSP - Travelling Salesman Problem). Dla ustalenia uwagi, sprecyzujemy tu jeden z wariantów TSP :
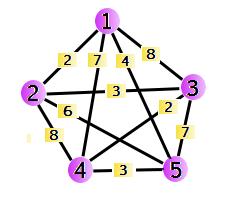
Ten problem jest trudny i nie jest znany algorytm, który rozwiązywałby go i działał w czasie wielomianowym. Wobec tego zaatakujemy problem, znajdując w miarę dobre rozwiązanie w czasie wykładniczym. Oczywiście nietrudno znaleźć rozwiązanie w czasie Rozważmy na potrzeby przykładu poniższy graf:
Dobrą praktyką, towarzyszącą wymyśleniu algorytmu programowania dynamicznego, jest próba wyszczególnienia pewnych stanów i konstrukcja rozwiązania dla każdego z nich z wykorzystaniem uprzednio obliczonych rozwiązań dla stanów poprzedzających. Tutaj naturalne jest zasymulowanie „podróży” komiwojażera przez wierzchołki grafu. Naszym stanem może być pewien fragment przebytej drogi. Moglibyśmy przyjąć, że stan to fragment drogi od pierwszego wierzchołka na jej trasie. Jednak taki pomysł nie różni się od brutalnego sprawdzania wszystkich permutacji. Tu pojawia się ważna obserwacja - jeśli rozpatrujemy pewien fragment ścieżki komiwojażera oraz wiemy w jakim miejscu się rozpoczął i w jakim zakończył, to nie jest dla nas istotne, w jakiej kolejności zostały odwiedzone pozostałe wierzchołki na ścieżce - istotne jest jedynie, które wierzchołki zostały już odwiedzone, szukamy wszak najlepszej spośród wszystkich tych możliwości i interesuje nas koszt, a nie kolejność. To odpowiada pomysłowi z wykorzystaniem nieuporządkowanych podzbiorów jako stanów - określmy stan (fragment ścieżki) jako podzbiór zbioru wszystkich wierzchołków, z wyszczególnionym początkiem i końcem. Szybko dochodzimy też do pomysłu na optymalizację tego podejścia - skoro (w naszym wariancie) ścieżka komiwojażera ma być cyklem, i przechodzić przez wszystkie wierzchołki, to bez straty ogólności możemy założyć, że zawsze zaczyna się ona w pewnym wyszczególnionym wierzchołku (nazwijmy go wierzchołkiem początkowym). W ten sposób przestrzeń stanów można ograniczyć do podzbiorów zbioru wierzchołków, wraz z wyszczególnionym wierzchołkiem końcowym. Teraz, szacując złożoność pamięciową, otrzymujemy
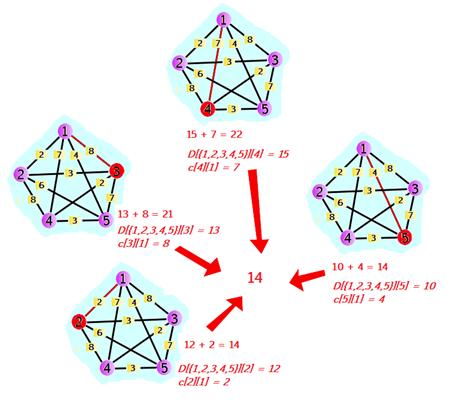
Teraz, skoro przebyliśmy drogę jedynie poprzez wierzchołki z podzbioru
Gdy dokonamy tych obliczeń dla wszystkich podzbiorów, otrzymamy najmniejsze wartości ścieżek, przebiegających wszystkie wierzchołki grafu, i kończących się w pewnym jego wierzchołku, różnym od 1. Teraz należy zamknąć cykl komiwojażera, powracając do wierzchołka nr 1. Stąd rozwiązanie to:
Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto.
(7 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


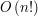 , bazujące na przejrzeniu wszystkich możliwych ścieżek, poprzez ustawienie wierzchołków na ścieżce za pomocą permutacji zbioru wierzchołków. Istnieje jednak sposób rozwiązania tego problemu, działający w czasie
, bazujące na przejrzeniu wszystkich możliwych ścieżek, poprzez ustawienie wierzchołków na ścieżce za pomocą permutacji zbioru wierzchołków. Istnieje jednak sposób rozwiązania tego problemu, działający w czasie 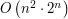 .
.
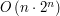 możliwych stanów.
możliwych stanów.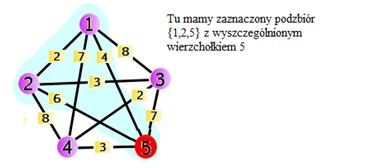
![$ l\left[w\right]\left[v\right] $](/files/tex/b28300e629631f8fa3b3ff19ecf7007ff12b8145.png) - waga ścieżki od wierzchołka
- waga ścieżki od wierzchołka 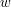 do wierzchołka
do wierzchołka 
![$ d\left[K\right]\left[v\right] $](/files/tex/95f8f57c3b3db8f5df67e0d7bdb9766988e4d6bc.png) - waga najkrótszej ścieżki, rozpoczynającej się w wierzchołku nr 1, przechodzącej przez wszystkie wierzchołki z podzbioru
- waga najkrótszej ścieżki, rozpoczynającej się w wierzchołku nr 1, przechodzącej przez wszystkie wierzchołki z podzbioru 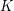 dokładnie raz i kończącej się w wierzchołku
dokładnie raz i kończącej się w wierzchołku 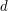 :
:![$ d\left[1\right]\left[1\right] = 0 $](/files/tex/4a3440bef2d0f70269ef2ac3686ad0d9c9d30e9a.png)
![$ d\left[\left\{1,w\right\}\right] = l\left[1\right]\left[w\right] $](/files/tex/f4030db8f742c13b6c5aebe3c69d7ef1572ad638.png)
![$ d\left[K\right]\left[w\right] = min\left\{d\left[K/\left\{w\right\}\right]\left[v\right]+l\left[v\right]\left[w\right]\left|\:v\in K/\left\{w,1\right\} \right\} \:dla\:w\neq1 $](/files/tex/9338263e587610f3f512eceadabcdb5b59d23bbe.png)
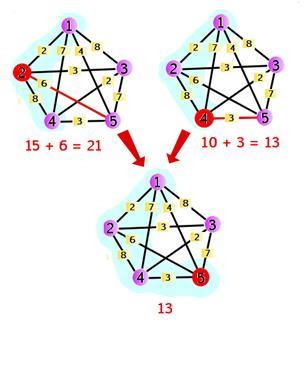
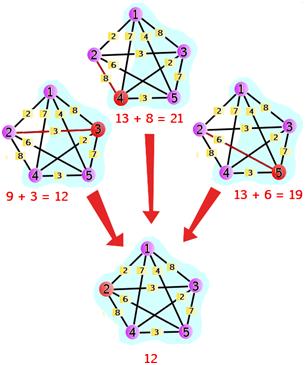
![$ min\left\{d\left[\left\{1,2,...,n\right\}\right]\left[v\right]+l\left[v\right]\left[1\right]\left|\:v\in\left\{2,3,...,n\right\}\right\} $](/files/tex/531efba38b9fc86476c206fe522f6537f3f80269.png)