PageRank, czyli jak Google stał się bogaty
28.09.2009 - Krzysztof Dryś
  Rozwiązaniem jest...Czy na portal temperowanie-olowkow.pl ludzie wchodzą tylko ze stron do niego linkujących? Czy opuszczając go zawsze przechodzą na strony, do których on linkuje? Oczywiście, że nie! Czasami ludzi wpisują w pasek wyszukiwania jakiś adres, a czasami korzystają z linków podesłanych przez znajomych.
Czy założenie, że na każdą stronę ludzie teleportują się jednakowo często, jest sensowne? Na pewno trochę kłóci się z naszą intuicją. Należy jednak cały czas mieć w pamięci, że chodzi nam tylko o niezły model.
...teleportacja!
Jeżeli uznamy, że ludzie poruszający się po linkach chodzą po sieci, to odpowiednią nazwą dla skakania do nowego adresu jest teleportacja. Niech
Wróćmy do naszego ostatniego przykładu. Jak zmieni się popularność stron po wprowadzeniu teleportacji? Załóżmy, że
Uwaga!
Do tej pory nasz model zależał tylko od tego, jak strony wzajemnie do siebie linkują. Od teraz będzie zależał jeszcze od parametru
 . .
W podobny sposób można zapisać równania dla pozostałych stron. Przyjmijmy, dla uproszczenia rachunków, że
PageRank to algorytm obliczający popularność strony w internecie. A PageRank strony internetowej to właśnie jej popularność, wyliczona w omawianym tutaj modelu. Czyli algorytm PageRank wylicza współczynnik PageRank dla różnych stron internetowych.
Odrobina matematykiNajpierw zobaczyliśmy przykład grafu dla którego łatwo ułożyć układ równań rozwiązać je i uszeregować strony względem popularności. Potem przekonaliśmy się, że są grafy w których nie jest to takie proste - nawet jeżeli rozwiążemy równania, to nie umiemy jeszcze powiedzieć, które strony są popularne. Na koniec zobaczyliśmy, że ostatnim wypadku pomoże nam teleportacja, która sprawiła, że strony znowu da się uszeregować względem popularności. Czy jednak tak jest zawsze? Okazuje się, że tak! Przy pomocy teorii spacerów losowych da się dowieść, że jeżeli tylko parametr teleportacji jest większy od 0, to po rozwiązaniu równań zawsze będziemy umieli uszeregować strony. I po kłopocie!Nareszcie udało się nam rozwiązać nasze równania. W ten sposób umiemy już uporządkować strony w internecie względem ich popularności. Podsumujmy to, co wiemy już o algorytmie PageRank. Działa on w następujący sposób:
Szybkość ma znaczenieWydaje się Wam, że wiemy już wszystko co potrzeba o algorytmie PageRank? To niestety nie jest prawda. Wciąż nie wiemy jak poradzić sobie z trzecim krokiem. Oczywiście znane są algorytmy rozwiązujące równania. Ale są one zdecydowanie za wolne! Pamiętajcie, że internet jest bardzo duży -- jest w nim ponad 100 miliardów stron. Możecie sobie wyobrazić, że rozwiązywanie równań, które mają 100 miliardów niewiadomych jest bardzo trudne. (3 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


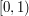 . Załóżmy, że jeżeli ktoś przegląda jakąś stronę to w
. Załóżmy, że jeżeli ktoś przegląda jakąś stronę to w 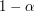 przypadków zwyczajnie podąża on jednym z linków na tej stronie.
przypadków zwyczajnie podąża on jednym z linków na tej stronie.
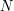 oznacza ilość wszystkich ludzi przeglądających internet. Wartość
oznacza ilość wszystkich ludzi przeglądających internet. Wartość 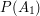 wciąż zależy od
wciąż zależy od 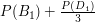 jednak teraz, z powodu teleportacji, zależy również od
jednak teraz, z powodu teleportacji, zależy również od 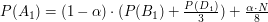 Skąd się wziął ten wzór? Popatrzmy na ludzi na stronach
Skąd się wziął ten wzór? Popatrzmy na ludzi na stronach 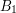 i
i 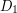 . Mogą oni opuścić aktualnie oglądane strony albo za pomocą normalnych linków, albo za pomocą teleportacji. Spośród nich
. Mogą oni opuścić aktualnie oglądane strony albo za pomocą normalnych linków, albo za pomocą teleportacji. Spośród nich 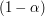 procent wybierze pierwsze rozwiązanie. Natomiast na dowolnej stronie (łącznie z
procent wybierze pierwsze rozwiązanie. Natomiast na dowolnej stronie (łącznie z 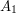 )
)  procent odwiedzających korzysta z teleportacji. Każdy teleportujący się ma szansę
procent odwiedzających korzysta z teleportacji. Każdy teleportujący się ma szansę 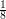 trafić na stronę
trafić na stronę 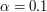 . Wtedy rozwiązaniem równań będzie (z dokładnością do trzech miejsc po przecinku):
. Wtedy rozwiązaniem równań będzie (z dokładnością do trzech miejsc po przecinku):
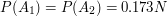
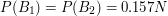
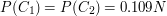
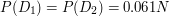 Znowu uda się nam uszeregować strony względem popularności.
Znowu uda się nam uszeregować strony względem popularności.


