PageRank, czyli jak Google stał się bogaty
28.09.2009 - Krzysztof Dryś
  Internetowy surferŻeby poradzić sobie z tym problemem spróbujemy zupełnie nowego podejścia. Pomoże nam w tym internetowy surfer. Wyobraźcie sobie człowieka, który zaraz po wstaniu rano włącza komputer i zaczyna przeglądać internet. Rozpoczyna to od wejścia na dowolną, losową, stronę internetową. Jest na niej minutę, a następnie podąża za jednym linków zamieszczonych na tej stronie. Na następnej stronie również przebywa chwilę i również opuszcza ją jednym z zamieszonych linków. Od czasu do czasu zamiast podążyć linkiem przechodzi na losową stronę w internecie. W ten sposób postępuje bez końca. Można to zapisać w ten sposób:
Topologia sieci to brzmiące mądrze określenie na strukturę linków między stronami.
Pamiętacie jak obliczaliśmy wartość PageRank strony? Najpierw tworzyliśmy układ równań wynikający z topologii sieci. Potem dodawaliśmy równanie
Przyjmijmy teraz, że łączna popularność wszystkich stron w internecie wynosi 1. Oznacza to, że
Po co to wszystko? Załóżmy, że surfer przegląda internet już od
Okazuje się jednak, że gdy Spójrzmy na to inaczej
Co tak właściwie oznacza ostatnie zdanie? Wyobraźmy sobie następujące doświadczenie losowe: bierzemy kostkę 10-ścienną i rzucamy nią
Popatrzmy na rysunek poniżej. Widać na nim wynik 10 doświadczeń losowych polegających na rzuceniu kostką sto tysięcy razy. Na osi pionowej zaznaczone ile razy, względem liczby dotychczasowych rzutów, wypadła jedynka. Jak wygląda ten wykres? Widzimy, że na początku wszystkie zależności oscylują daleko od 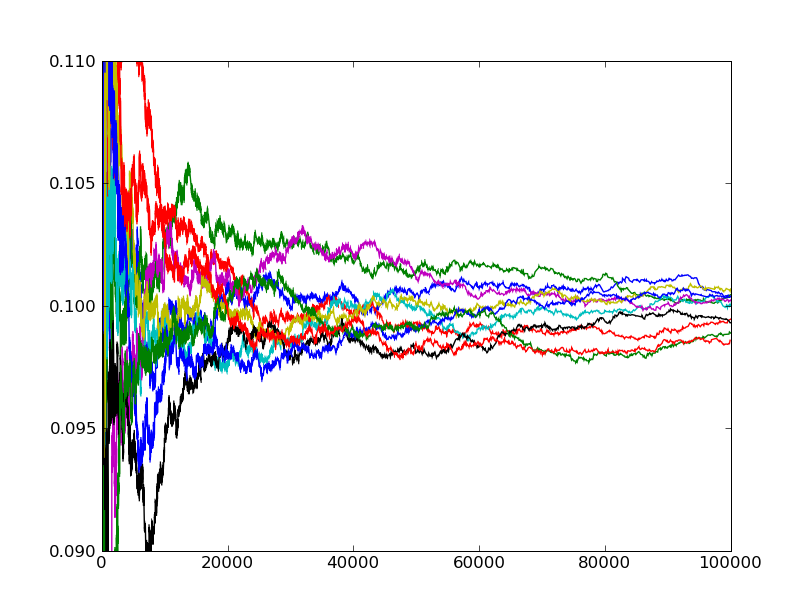 Ile razy wypadnie jedynka, jeżeli będziemy rzucali kostką 10-ścienną? Powinna wypadać w około
Ile razy wypadnie jedynka, jeżeli będziemy rzucali kostką 10-ścienną? Powinna wypadać w około 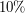 rzutów. Widzimy, że im więcej razy rzucimy kostką, tym bardziej zbliżamy się do tej wartości. rzutów. Widzimy, że im więcej razy rzucimy kostką, tym bardziej zbliżamy się do tej wartości.
Na następnym rysunku widać wynik 10 prób losowych, polegających na spacerze naszego surfera po grafie z ostatniego przykładu. Na osi pionowej zaznaczone jest 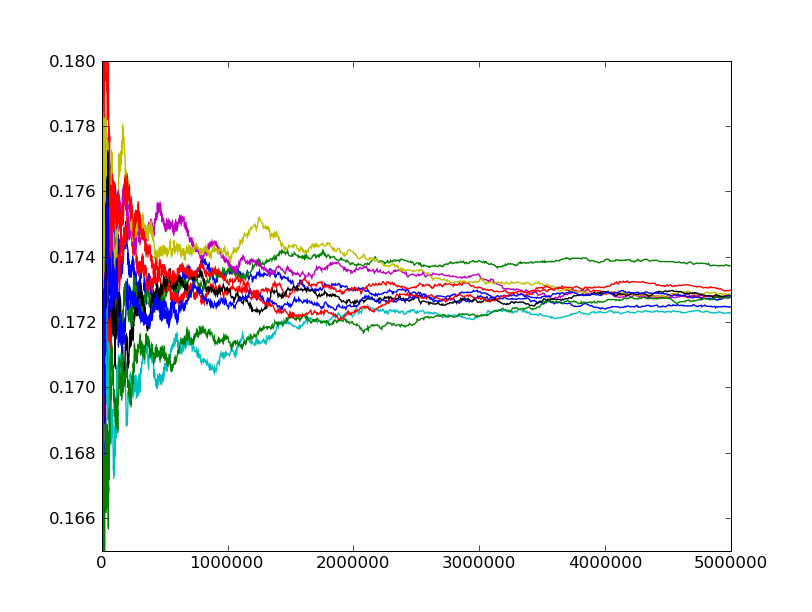 Ile razy surfer internetowy odwiedzi stronę
Ile razy surfer internetowy odwiedzi stronę  podczas chodzenia losowego po internecie? Matematyka mówić, że po podczas chodzenia losowego po internecie? Matematyka mówić, że po  turach powinien być tam około turach powinien być tam około 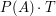 razy. Podobnie jak w przypadku rzutów kostka widzimy, że im większe razy. Podobnie jak w przypadku rzutów kostka widzimy, że im większe  , tym bliżej tej wartości jesteśmy. , tym bliżej tej wartości jesteśmy.
(3 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


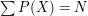 , gdzie sumowanie przebiega po wszystkich stronach, a
, gdzie sumowanie przebiega po wszystkich stronach, a 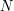 to łączna popularność wszystkich stron w sieci. Na końcu rozwiązywaliśmy układ równań i dostawaliśmy wszystkie współczynniki.
to łączna popularność wszystkich stron w sieci. Na końcu rozwiązywaliśmy układ równań i dostawaliśmy wszystkie współczynniki.
 spełnia następujące równanie:
spełnia następujące równanie: 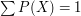
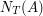 razy. Oczywiście, wartość
razy. Oczywiście, wartość 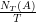 jest coraz bliższe
jest coraz bliższe 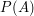 .
.
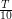 . Natomiast, jeżeli
. Natomiast, jeżeli 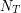 oznacza ilość jedynek po
oznacza ilość jedynek po 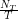 będzie blisko
będzie blisko 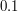 .
.
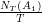 . Czyli ile razy, względem ilości czasu, który do tej pory upłynął, surfer był na stronie
. Czyli ile razy, względem ilości czasu, który do tej pory upłynął, surfer był na stronie 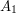 .
.


