Autostrady

Jednym z moich ulubionych zadań z konkursów informatycznych są ,,Autostrady'' z II etapu X Olimpiady Informatycznej 2002/2003. Jego treść (obrana z historyjki) wygląda mniej więcej tak: Na prostej wybrano punktów ponumerowanych od do według ich kolejności występowania na tej prostej. Danych jest par punktów, które należy połączyć łukami. Każdy taki łuk musi przebiegać w całości po jednej stronie prostej. Ponadto łuki nie mogą się przecinać -- mogą się jedynie łączyć na końcach. Napisz program, który zdecyduje, po której stronie prostej poprowadzić łuki, aby się nie przecinały, lub stwierdzi, że nie jest to możliwe.

Zadanie to ma bardzo prostą interpretację grafową. Wierzchołkami grafu są pary punktów, które chcemy połączyć łukiem (w dalszej części będę je nazywał po prostu łukami). Dwa wierzchołki są połączone krawędzią, gdy odpowiadające im łuki umieszczone po tej samej stronie prostej przecinają się. Odpowiednie rozmieszczenie łuków sprowadza się do pokolorowania wierzchołków tego grafu dwoma kolorami w taki sposób, aby wierzchołki tego samego koloru nie były połączone krawędzią (takie kolorowanie nazywamy poprawnym). Wówczas jeden kolor wskazuje, które łuki poprowadzić po jednej stronie, a drugi kolor -- po drugiej stronie prostej.

Pojawia się jednak istotny problem: taki graf może mieć rozmiar kwadratowy. Ograniczenia na rozmiar danych wejściowych jasno wskazują, że złożoność kwadratowa jest w tym zadaniu niewystarczająca. Czy to oznacza, że musimy zrezygnować z podejścia grafowego? Bynajmniej.

Naszym celem jest poprawne pokolorowanie grafu przecięć dwoma kolorami. Takie kolorowanie, o ile istnieje, jest zdeterminowane przez jakikolwiek spójny podgraf rozpinający (tj. posiadający ten sam zbiór wierzchołków), na przykład drzewo. Jeżeli graf przecięć jest niespójny, to dwukolorowanie jest zdeterminowane na każdej spójnej składowej przez drzewo rozpinające tę składową. Poprawne dwukolorowanie drzewa rozpinającego niekoniecznie jest poprawnym dwukolorowaniem całej składowej, ale jeżeli nie jest, to składowa ta w ogóle nie jest dwukolorowalna. Jak zatem wygląda algorytm? Zamiast pełnego grafu przecięć, znajdujemy las drzew rozpinających jego spójne składowe (w skrócie: las przecięć). Następnie kolorujemy go poprawnie dwoma kolorami, po czym sprawdzamy, czy otrzymane kolorowanie jest poprawnym kolorowaniem całego grafu, a więc czy łuki poprowadzone po odpowiednich stronach prostej danych przez kolory wierzchołków rzeczywiście się nie przecinają. Takie sprawdzenie jest już łatwe -- analogiczne do sprawdzenia poprawności wyrażenia nawiasowego.

Jedyną kwestią, która pozostała do rozwiązania, jest szybkie znajdowanie lasu przecięć. Rozwiązanie wzorcowe z OI dodaje nowe łuki do lasu przecięć w dowolnej kolejności, używając do tego celu zrównoważonego drzewa przeszukiwań binarnych wzbogaconego o pewne dodatkowe informacje, przez co jest dość skomplikowane i trudne w implementacji. Ja rozumowałem następująco: skoro wszystkie łuki są znane od początku, to możemy je wstępnie posortować, co powinno uprościć dalszą część algorytmu. Sortujemy więc łuki w kolejności rosnących lewych końców, a w przypadku równości -- malejących prawych końców, a następnie w tej kolejności dodajemy je do konstruowanego lasu przecięć.

Aktualnie rozpatrywany i dodawany do lasu przecięć łuk nazwijmy nowym łukiem. Niech będzie jego lewym końcem. Przypatrzmy się spójnym składowym dotychczas skonstruowanego lasu. W każdej składowej możemy pominąć wszystkie łuki, które nie sięgają poza , gdyż nie wygenerują już żadnych nowych przecięć (jeżeli żaden łuk nie sięga poza , to pomijamy całą składową). Ten spośród pozostałych łuków, który ma najmniejszy prawy koniec, nazwijmy reprezentantem składowej. Jeżeli nowy łuk przecina jakąś składową, to przecina jej reprezentanta (przykład na rysunku). Wówczas do lasu przecięć dodajemy krawędź łączącą nowy łuk z reprezentantem.

,,Interesujące'' składowe (te, które sięgają poza ) przechowujemy na stosie. Na szczycie stosu jest składowa najbliższa . Najpierw przecinamy ją z nowym łukiem poprzez dodanie krawędzi łączącej go z reprezentantem. Następnie zdejmujemy ją ze stosu i przecinamy z nowym łukiem kolejną składową na stosie. Robimy to dopóty, dopóki nowy łuk przecina reprezentanta składowej na szczycie stosu. Wszystkie zdjęte ze stosu składowe i nowy łuk łączymy w jedną składową, którą na końcu odkładamy na stos. Jej reprezentantem staje się ten łuk, który w całej nowej składowej ma najmniejszy prawy koniec (zaznaczone łuki na poniższym rysunku to właśnie reprezentanci).

Zobaczmy, co się dokładnie dzieje ze składowymi w powyższym algorytmie. W każdej składowej znajdujemy jej reprezentanta (łuk o najmniejszym prawym końcu), czasem (kiedy się zwiększa) tego reprezentanta usuwamy i czasem łączymy dwie składowe w~jedną większą. Właściwą strukturą danych dla tych operacji jest tzw. kolejka złączalna -- struktura, która umożliwia znajdowanie minimum, usuwanie minimum oraz łączenie kilku struktur w jedną.

Najprostszą implementacją kolejki złączalnej jest drzewo lewicowe. W drzewie tym wartości przechowywane w węzłach spełniają warunek kopca (wartość w węźle jest nie większa niż wartości w jego dzieciach), a ponadto w każdym poddrzewie skrajnie prawa ścieżka jest najkrótsza ze wszystkich ścieżek od korzenia do liścia zewnętrznego (jest to umowny węzeł, który występuje wszędzie tam, gdzie nie ma syna). Ta ostatnia własność implikuje, że ścieżka ta ma logarytmiczną długość. Łączenie dwóch takich drzew sprowadza się do scalenia ich skrajnie prawych ścieżek z zachowaniem warunku kopca, a następnie przywrócenia ,,lewicowości'' poprzez zamianę miejscami synów w pewnych węzłach tej (scalonej) ścieżki -- wszystko odbywa się w czasie logarytmicznym. Element minimalny oczywiście leży w korzeniu drzewa. Jego usunięcie sprowadza się do połączenia poddrzew obu jego synów.

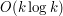Poniżej załączam pełny kod mojego rozwiązania. Algorytm działa w czasie , a jego implementacja jest krótka i elegancka. Na zawodach jako jedyny uzyskałem maksymalną liczbę 100 punktów za to zadanie, a to zawsze szczególnie cieszy :)

#include <iostream>
#include <list>
#include <vector>
#include <stack>
#include <algorithm>
using namespace std;

struct road {
    int from, to;
    list adj;
    int color, number;
    
    road():color(-1) {}
};

struct tree_node {
    tree_node *left, *right;
    int len;
    road *rd;
    
    tree_node(road *rdi):left(0), right(0), len(1), rd(rdi) {}
};

tree_node *union_trees(tree_node *a, tree_node *b) {
    if (a->rd->to > b->rd->to) swap(a, b);
    a->left = a->left ? union_trees(a->left, b) : b;
    if (!a->right || a->left->len > a->right->len) swap(a->left, a->right);
    a->len = a->left ? a->left->len+1 : 1;
    return a;
}

bool operator<(const road &a, const road &b) {
    return a.from < b.from || a.from == b.from && a.to > b.to;
}

void search(road *current, int c) {
    if (current->color != -1) return;
    current->color = c;
    for (list::iterator i = current->adj.begin();
         i != current->adj.end(); ++i) search(*i, c^1);
}

int main() {
    int n, k;
    cin >> n >> k;
    vector roads(k);
    for (int i = 0; i < k; ++i) {
        cin >> roads[i].from >> roads[i].to;
        roads[i].number = i;
    }
    sort(roads.begin(), roads.end());
    stack S;
    for (int i = 0; i < k; ++i) {
        while (!S.empty() && S.top()->rd->to <= roads[i].from) {
            tree_node *root = S.top();
            if (root->left) S.top() = union_trees(root->left, root->right);
            else if (root->right) S.top() = root->right;
            else S.pop();
            delete root;
        }
        tree_node *cur = new tree_node(&roads[i]);
        while (!S.empty() && S.top()->rd->to < roads[i].to) {
            S.top()->rd->adj.push_back(&roads[i]);
            roads[i].adj.push_back(S.top()->rd);
            cur = union_trees(cur, S.top());
            S.pop();
        }
        S.push(cur);
    }
    for (int i = 0; i < k; ++i) search(&roads[i], 0);
    stack side[2];
    for (int i = 0; i < k; ++i) {
        int c = roads[i].color;
        while (!side[c].empty() && side[c].top()->to <= roads[i].from)
          side[c].pop();
        if (!side[c].empty() && side[c].top()->to < roads[i].to) {
            cout << "NIE" << endl;
            return 0;
        }
        side[c].push(&roads[i]);
    }
    vector colors(k);
    for (int i = 0; i < k; ++i) colors[roads[i].number] = roads[i].color;
    for (int i = 0; i < k; ++i) cout << (colors[i] ? 'S' : 'N') << endl;
    return 0;
}