Jednym z najciekawszych zadań spośród tych, nad którymi miałem okazję się chwilę zastanawiać, są Krasnoludki. Problem pochodzi z obozu treningowego na IOI drużyny reprezentującej Rumunię, a odnalazłem o nim informację poprzez wpis na blogu Mihai'a Pătraşcu (na którym można znaleźć także wiele innych ciekawych problemów!).
Zadanie
Historia zadania opowiada o  krasnoludkach, które w bliżej niewyjaśnionych okolicznościach wpadły do głębokiej na
krasnoludkach, które w bliżej niewyjaśnionych okolicznościach wpadły do głębokiej na 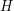 metrów dziury. Niestety nie mają przy sobie żadnych narzędzi czy lin... mogą więc liczyć tylko na utworzenie żywej wieży, gdzie każdy krasnoludek staje na barkach poprzednika. Gdy krasnoludek dosięga ramionami powierzchni ziemi może się już uwolnić, niestety z niezrozumiałych, acz ściśle zastrzeżonych w treści zadania powodów, nie może już w takim przypadku udzielać żadnej pomocy pozostałym krasnoludkom (trzeba przyznać, że nie świadczy to o nich najlepiej...). Każdy krasnoludek jest charakteryzowany wysokością od ziemi do barków
metrów dziury. Niestety nie mają przy sobie żadnych narzędzi czy lin... mogą więc liczyć tylko na utworzenie żywej wieży, gdzie każdy krasnoludek staje na barkach poprzednika. Gdy krasnoludek dosięga ramionami powierzchni ziemi może się już uwolnić, niestety z niezrozumiałych, acz ściśle zastrzeżonych w treści zadania powodów, nie może już w takim przypadku udzielać żadnej pomocy pozostałym krasnoludkom (trzeba przyznać, że nie świadczy to o nich najlepiej...). Każdy krasnoludek jest charakteryzowany wysokością od ziemi do barków 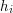 , oraz zasięgiem ramion
, oraz zasięgiem ramion 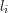 . Naszym zadaniem jest na podstawie danej wysokości dziury
. Naszym zadaniem jest na podstawie danej wysokości dziury 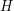 oraz opisów
oraz opisów  krasnoludków
krasnoludków 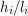 wyznaczyć ile maksymalnie krasnoludków może się uratować z tej opresji.
Przykładowo, dla dziury o wysokości
wyznaczyć ile maksymalnie krasnoludków może się uratować z tej opresji.
Przykładowo, dla dziury o wysokości 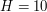 oraz czterech krasnoludków
oraz czterech krasnoludków
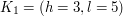 ,
,
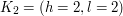 ,
,
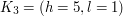 ,
,
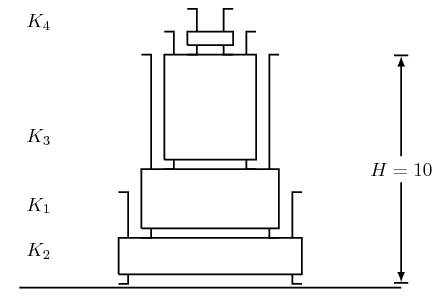
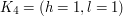 możemy uratować 3 krasnoludki ustawiając je w kolejności
możemy uratować 3 krasnoludki ustawiając je w kolejności 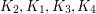 , tak jak na rysunku:
, tak jak na rysunku:
Pierwsze podejście - algorytmy zachłanne
Pierwszy pomysłem, który próbowałem w tym zadaniu zastosować, to wyznaczenie strategii zachłannej. Niestety każde proste kryterium okazywało się w tym wypadku zawodne (np. uporządkowanie kolejności krasnoludków na wieży według malejących wartości 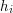 lub sum
lub sum 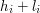 ). Co ciekawe, gdyby krasnoludki były opisywane tylko przez jedną wartość
). Co ciekawe, gdyby krasnoludki były opisywane tylko przez jedną wartość 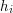 (czyli
(czyli 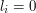 ), to zadanie staje się bardzo proste, wystarczy uporządkować je według malejących wartości
), to zadanie staje się bardzo proste, wystarczy uporządkować je według malejących wartości 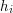 i wyznaczyć minimalny indeks
i wyznaczyć minimalny indeks  taki, że
taki, że 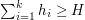 .
.
Gdybyśmy dysponowali magiczną skrzynką, która potrafiłaby odpowiadać, czy w optymalnym rozwiązaniu
dany krasnolud musi zostać "poświęcony" dla dobra ogółu (czyli zostanie na dnie dziury), czy też uda się go uratować, to do konstrukcji optymalnego rozwiązania możemy już zastosować algorytm zachłanny.
Wszystkie krasnoludy, których nie uda się uratować, możemy ustawić na dole wieży, pozostałe krasnoludki ustawiamy w kolejności malejących sum 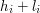 (czyli krasnoludki o najwyższej sumie są najniżej w wieży, a te o najmniejszej sumie najwyżej). Konieczne jest wykazania, że dowolne rozwiązanie, możemy sprowadzić do równie dobrego (czyli ratującego ten sam zbiór krasnoludków), w którym uratowane krasnoludki uporządkowane są według malejących wartości
(czyli krasnoludki o najwyższej sumie są najniżej w wieży, a te o najmniejszej sumie najwyżej). Konieczne jest wykazania, że dowolne rozwiązanie, możemy sprowadzić do równie dobrego (czyli ratującego ten sam zbiór krasnoludków), w którym uratowane krasnoludki uporządkowane są według malejących wartości 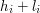 .
.
Pierwsza część powyższego stwierdzenie jest dosyć oczywista, jeśli umieścimy krasnoludka, który musi zostać "poświęcony" w środku wieży, to równie dobrze możemy go przenieść na sam spód wieży, co spowoduje że:
- uratowanie krasnoludków, które znajdowały się poniżej, będzie łatwiejsze, po zmianie będą znajdować się wyżej niż poprzednio,
- pozycja krasnoludków, które znajdowały się powyżej pozostanie bez zmian.
Tak więc taka zmiana nie pogorszy obecnego rozwiązania (a może je nawet polepszyć).
Druga cześć twierdzenia wymaga dokładniejszej analizy, jednak dowód jest również bardzo prosty. Załóżmy, że jeśli w pewnym rozwiązaniu na wieży sąsiadują dwa krasnoludki o opisach 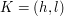 (na wysokości
(na wysokości  w wieży) oraz
w wieży) oraz 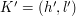 (na wysokości
(na wysokości 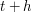 w wieży), takie, że
w wieży), takie, że 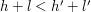 . Ponieważ możemy uratować oba krasnoludki stąd:
. Ponieważ możemy uratować oba krasnoludki stąd: 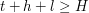 oraz
oraz 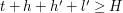 . Zamiana krasnoludków miejscami w żaden sposób nie wpływa na sytuację pozostałych krasnoludków, dodatkowo po tej zamianie nadal możemy uratować
. Zamiana krasnoludków miejscami w żaden sposób nie wpływa na sytuację pozostałych krasnoludków, dodatkowo po tej zamianie nadal możemy uratować 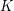 i
i 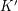 :
:
Niestety nie dysponujemy taka magiczną skrzynką (jeszcze!), koniecznie jest więc dalsze poszukiwanie rozwiązania. Jednak poprzednia obserwacja będzie bardzo przydatna w konstrukcji poprawnego rozwiązania.
Drugie podejście - programowanie dynamiczne
Skoro użycie strategii zachłannej zakończyło się porażką, to może warto spróbować programowania dynamicznego. Niestety musimy zmierzyć się z dwoma problemami:
- Po pierwsze, treść zadania nie nakłada żadnych ograniczeń na wartości
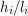 , czyli w szczególności mogą to być liczby rzeczywiste, co wyklucza możliwość budowania programowania w oparciu o wysokości wież, którą mogą otworzyć krasnoludki.
, czyli w szczególności mogą to być liczby rzeczywiste, co wyklucza możliwość budowania programowania w oparciu o wysokości wież, którą mogą otworzyć krasnoludki.
- Drugim problemem jest brak prostego kryterium pozwalającego rozszerzać już wyznaczone rozwiązanie o kolejne krasnoludki. Niekiedy nawet dodanie jednego krasnoludka powoduje duże zmiany w rozwiązaniu.
Niestety powyższe problemy powodują, że i w tym przypadku trzeba przyznać się do porażki.
Połączenie obu rozwiązań
Zazwyczaj w programowaniu dynamicznym nie ma znaczenia w jakim porządku analizujemy dane (czyli w naszym wypadku krasnoludki), jednak w tym zadaniu jest to kluczowe.
W pierwszym kroku porządkujemy malejąco krasnoludki według sum 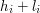 , czyli od tego momentu może zakładać, że
, czyli od tego momentu może zakładać, że 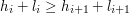 dla
dla 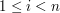 . Dzięki takiemu postępowaniu będzie możliwe rozszerzanie już wyznaczonych rozwiązań o kolejne krasnoludki.
. Dzięki takiemu postępowaniu będzie możliwe rozszerzanie już wyznaczonych rozwiązań o kolejne krasnoludki.
Zdefiniujmy wartości ![$ M[i,u] $](/files/tex/aeeb970e2170be87dd6caa8731f220c74ddf9567.png) , dla
, dla 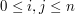 oznaczające maksymalną wysokość dziury, dla której możliwe jest uratowanie
oznaczające maksymalną wysokość dziury, dla której możliwe jest uratowanie  krasnoludków spośród krasnoludków o numerach
krasnoludków spośród krasnoludków o numerach 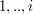 . Wartości brzegowe możemy zdefiniować zakładając, że
. Wartości brzegowe możemy zdefiniować zakładając, że ![$ M[i,0]=\infty $](/files/tex/7c697a20c1c251c484e5beff72f5759119d74b50.png) , oraz
, oraz ![$ M[0,u]=-\infty $](/files/tex/68aec21acbea4811d629cc99a517e1063eb613d8.png) (co oznacza brak rozwiązania), dla
(co oznacza brak rozwiązania), dla 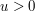 .
.
Szczęśliwie wartości ![$ M[i,u] $](/files/tex/aeeb970e2170be87dd6caa8731f220c74ddf9567.png) dla
dla 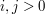 można wyznaczyć na podstawie wartości
można wyznaczyć na podstawie wartości ![$ M[i-1,u] $](/files/tex/1c609c828e3ad4eb7015d2f0b753e4aa5545a013.png) oraz
oraz ![$ M[i-1,u-1] $](/files/tex/a3cfcdc5c5bcae629dfd94deee5405e46a2b58f8.png) . Otóż dla
. Otóż dla ![$ M[i,u] $](/files/tex/aeeb970e2170be87dd6caa8731f220c74ddf9567.png) musimy podjąć decyzję czy krasnoludek o numerze
musimy podjąć decyzję czy krasnoludek o numerze  -tym powinien zostać uratowany czy też niestety nie. Jeśli nie decydujemy się na jego uratowanie, to
-tym powinien zostać uratowany czy też niestety nie. Jeśli nie decydujemy się na jego uratowanie, to  -tego krasnoludka możemy ustawić na spodzie wieży, stąd nowe rozwiązanie będzie miało wysokość
-tego krasnoludka możemy ustawić na spodzie wieży, stąd nowe rozwiązanie będzie miało wysokość ![$ m_1 = M[i-1,u]+h_i $](/files/tex/3b430b34f313f20e4475927ca88ced8e1defe233.png) . Natomiast jeśli chcemy jednak uratować
. Natomiast jeśli chcemy jednak uratować  -tego krasnoludka, to powinniśmy umieścić go na szczycie wieży (tutaj korzystamy z obserwacji z algorytmu zachłannego!). Wysokość wieży będzie taka sama jak w przypadku
-tego krasnoludka, to powinniśmy umieścić go na szczycie wieży (tutaj korzystamy z obserwacji z algorytmu zachłannego!). Wysokość wieży będzie taka sama jak w przypadku ![$ M[i-1,u-1] $](/files/tex/a3cfcdc5c5bcae629dfd94deee5405e46a2b58f8.png) jeśli krasnoludek dosięga do szczytu dziury, lub
jeśli krasnoludek dosięga do szczytu dziury, lub 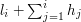 w przeciwnym przypadku, stąd wartość rozwiązania w tym przypadku wynosi
w przeciwnym przypadku, stąd wartość rozwiązania w tym przypadku wynosi ![$ m_2 = \min(M[i-1,u-1], l_i+\sum_{j=1}^i h_j) $](/files/tex/de1e9ee31e3d55f301e9e76a6d090dfd8e14ce72.png) .
Łącząc te dwa przypadki otrzymujemy:
.
Łącząc te dwa przypadki otrzymujemy: ![$ M[i,u]=\max(m_1,m_2) $](/files/tex/9bae16ac9e334569817387c78dff02f224b845fd.png) .
.
Maksymalną liczbę krasnoludków, którą można uratować można odczytać z tablicy 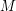 wybierając maksymalny indeks
wybierając maksymalny indeks  , taki, że
, taki, że ![$ M[n,u]\ge H $](/files/tex/5ef49c46860dfaf01bb28dd1491b7b2736045a51.png) .
.
Pełen opis algorytmu wyznaczającego tablicę 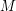 znajduje się poniżej. Łatwo sprawdzić, że jego złożoność czasowa to
znajduje się poniżej. Łatwo sprawdzić, że jego złożoność czasowa to 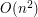 .
.
- uporządkuj krasnoludki, malejąco, według wartości
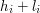
- wyznacz wartości
![$ H[i]=\sum_{j=1}^i h_i $](/files/tex/ea682666782a86017e0dfe54cdc66202929a43c4.png) dla
dla 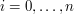
- for
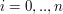
![$ M[i,0]=\infty $](/files/tex/7c697a20c1c251c484e5beff72f5759119d74b50.png) ,
, ![$ M[0,u]=-\infty $](/files/tex/68aec21acbea4811d629cc99a517e1063eb613d8.png) dla
dla 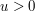
- for
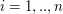
for 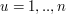 do
do
![$ m_1 = M[i-1,u]+h_i $](/files/tex/3b430b34f313f20e4475927ca88ced8e1defe233.png) jeśli
jeśli ![$ M[i-1,u]\ge 0 $](/files/tex/559d4da53cdc57b7b2b7b336a22905d8437180e0.png) lub
lub 
![$ m_2 = \min(H[i]+l_i, M[i-1,u-1]) $](/files/tex/fd301dcd405fd3274952dd81854eee4fa142b9d7.png) jeśli
jeśli ![$ M[i-1,u-1]\ge 0 $](/files/tex/4aeb617ece6054ae9bac8f65d17b16b792642e97.png) , lub
, lub 
![$ M[i,u] = \max(m_1,m_2) $](/files/tex/cc7465482c0eda07969469d386fe439eab91c157.png)
- return
![$ \max\{ u : M[n,u] \ge H $](/files/tex/e69be27b9ea92a60dd1b8f38fc7541983b83b158.png) dla
dla 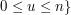






 krasnoludkach, które w bliżej niewyjaśnionych okolicznościach wpadły do głębokiej na
krasnoludkach, które w bliżej niewyjaśnionych okolicznościach wpadły do głębokiej na 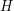 metrów dziury. Niestety nie mają przy sobie żadnych narzędzi czy lin... mogą więc liczyć tylko na utworzenie żywej wieży, gdzie każdy krasnoludek staje na barkach poprzednika. Gdy krasnoludek dosięga ramionami powierzchni ziemi może się już uwolnić, niestety z niezrozumiałych, acz ściśle zastrzeżonych w treści zadania powodów, nie może już w takim przypadku udzielać żadnej pomocy pozostałym krasnoludkom (trzeba przyznać, że nie świadczy to o nich najlepiej...). Każdy krasnoludek jest charakteryzowany wysokością od ziemi do barków
metrów dziury. Niestety nie mają przy sobie żadnych narzędzi czy lin... mogą więc liczyć tylko na utworzenie żywej wieży, gdzie każdy krasnoludek staje na barkach poprzednika. Gdy krasnoludek dosięga ramionami powierzchni ziemi może się już uwolnić, niestety z niezrozumiałych, acz ściśle zastrzeżonych w treści zadania powodów, nie może już w takim przypadku udzielać żadnej pomocy pozostałym krasnoludkom (trzeba przyznać, że nie świadczy to o nich najlepiej...). Każdy krasnoludek jest charakteryzowany wysokością od ziemi do barków 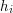 , oraz zasięgiem ramion
, oraz zasięgiem ramion 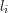 . Naszym zadaniem jest na podstawie danej wysokości dziury
. Naszym zadaniem jest na podstawie danej wysokości dziury 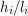 wyznaczyć ile maksymalnie krasnoludków może się uratować z tej opresji.
Przykładowo, dla dziury o wysokości
wyznaczyć ile maksymalnie krasnoludków może się uratować z tej opresji.
Przykładowo, dla dziury o wysokości 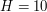 oraz czterech krasnoludków
oraz czterech krasnoludków
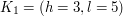 ,
,
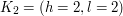 ,
,
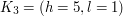 ,
,
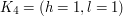 możemy uratować 3 krasnoludki ustawiając je w kolejności
możemy uratować 3 krasnoludki ustawiając je w kolejności 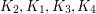 , tak jak na rysunku:
, tak jak na rysunku:
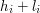 ). Co ciekawe, gdyby krasnoludki były opisywane tylko przez jedną wartość
). Co ciekawe, gdyby krasnoludki były opisywane tylko przez jedną wartość 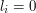 ), to zadanie staje się bardzo proste, wystarczy uporządkować je według malejących wartości
), to zadanie staje się bardzo proste, wystarczy uporządkować je według malejących wartości  taki, że
taki, że 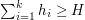 .
.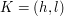 (na wysokości
(na wysokości  w wieży) oraz
w wieży) oraz 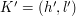 (na wysokości
(na wysokości 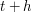 w wieży), takie, że
w wieży), takie, że 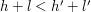 . Ponieważ możemy uratować oba krasnoludki stąd:
. Ponieważ możemy uratować oba krasnoludki stąd: 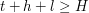 oraz
oraz 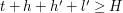 . Zamiana krasnoludków miejscami w żaden sposób nie wpływa na sytuację pozostałych krasnoludków, dodatkowo po tej zamianie nadal możemy uratować
. Zamiana krasnoludków miejscami w żaden sposób nie wpływa na sytuację pozostałych krasnoludków, dodatkowo po tej zamianie nadal możemy uratować 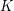 i
i 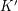 :
:
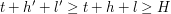
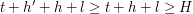
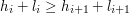 dla
dla 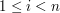 . Dzięki takiemu postępowaniu będzie możliwe rozszerzanie już wyznaczonych rozwiązań o kolejne krasnoludki.
. Dzięki takiemu postępowaniu będzie możliwe rozszerzanie już wyznaczonych rozwiązań o kolejne krasnoludki.![$ M[i,u] $](/files/tex/aeeb970e2170be87dd6caa8731f220c74ddf9567.png) , dla
, dla 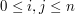 oznaczające maksymalną wysokość dziury, dla której możliwe jest uratowanie
oznaczające maksymalną wysokość dziury, dla której możliwe jest uratowanie  krasnoludków spośród krasnoludków o numerach
krasnoludków spośród krasnoludków o numerach 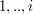 . Wartości brzegowe możemy zdefiniować zakładając, że
. Wartości brzegowe możemy zdefiniować zakładając, że ![$ M[i,0]=\infty $](/files/tex/7c697a20c1c251c484e5beff72f5759119d74b50.png) , oraz
, oraz ![$ M[0,u]=-\infty $](/files/tex/68aec21acbea4811d629cc99a517e1063eb613d8.png) (co oznacza brak rozwiązania), dla
(co oznacza brak rozwiązania), dla 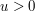 .
.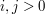 można wyznaczyć na podstawie wartości
można wyznaczyć na podstawie wartości ![$ M[i-1,u] $](/files/tex/1c609c828e3ad4eb7015d2f0b753e4aa5545a013.png) oraz
oraz ![$ M[i-1,u-1] $](/files/tex/a3cfcdc5c5bcae629dfd94deee5405e46a2b58f8.png) . Otóż dla
. Otóż dla  -tym powinien zostać uratowany czy też niestety nie. Jeśli nie decydujemy się na jego uratowanie, to
-tym powinien zostać uratowany czy też niestety nie. Jeśli nie decydujemy się na jego uratowanie, to ![$ m_1 = M[i-1,u]+h_i $](/files/tex/3b430b34f313f20e4475927ca88ced8e1defe233.png) . Natomiast jeśli chcemy jednak uratować
. Natomiast jeśli chcemy jednak uratować 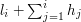 w przeciwnym przypadku, stąd wartość rozwiązania w tym przypadku wynosi
w przeciwnym przypadku, stąd wartość rozwiązania w tym przypadku wynosi ![$ m_2 = \min(M[i-1,u-1], l_i+\sum_{j=1}^i h_j) $](/files/tex/de1e9ee31e3d55f301e9e76a6d090dfd8e14ce72.png) .
Łącząc te dwa przypadki otrzymujemy:
.
Łącząc te dwa przypadki otrzymujemy: ![$ M[i,u]=\max(m_1,m_2) $](/files/tex/9bae16ac9e334569817387c78dff02f224b845fd.png) .
.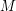 wybierając maksymalny indeks
wybierając maksymalny indeks ![$ M[n,u]\ge H $](/files/tex/5ef49c46860dfaf01bb28dd1491b7b2736045a51.png) .
.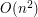 .
.![$ H[i]=\sum_{j=1}^i h_i $](/files/tex/ea682666782a86017e0dfe54cdc66202929a43c4.png) dla
dla 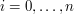
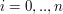
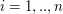
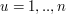 do
do![$ M[i-1,u]\ge 0 $](/files/tex/559d4da53cdc57b7b2b7b336a22905d8437180e0.png) lub
lub 
![$ m_2 = \min(H[i]+l_i, M[i-1,u-1]) $](/files/tex/fd301dcd405fd3274952dd81854eee4fa142b9d7.png) jeśli
jeśli ![$ M[i-1,u-1]\ge 0 $](/files/tex/4aeb617ece6054ae9bac8f65d17b16b792642e97.png) , lub
, lub ![$ M[i,u] = \max(m_1,m_2) $](/files/tex/cc7465482c0eda07969469d386fe439eab91c157.png)
![$ \max\{ u : M[n,u] \ge H $](/files/tex/e69be27b9ea92a60dd1b8f38fc7541983b83b158.png) dla
dla