Między zwycięstwem a porażką
28.08.2009 - Przemysław Pietrzkiewicz
 'Biada podrzędnym jednostkom, kiedy wejdą między ostrza potężnych szermierzy' - pisał pewien angielski dżentelmen*. W artykule opowiemy o tym co zrobić, aby to nam przypadła rola postaci z końca cytatu, choć szermierkę zastąpimy grami nie wymagającymi używania mieczy. Celem artykułu jest przedstawienie Czytelnikowi fundamentów ogromnej, fascynującej dziedziny, jaką jest teoria gier. Zapoczątkowana w XVIII wieku, współcześnie znajduje zastosowanie w ekonomii, polityce, wojskowości, a nawet biologii. U jej podstaw leżą bardzo proste techniki - zaprezentujemy je na przykładzie dwóch nieskomplikowanych gier. Nasz cel każdorazowo będzie identyczny - znaleźć strategię wygrywającą, czyli dowiedzieć się, jakie ruchy zapewnią nam zwycięstwo. Wyobraźmy sobie prostą grę planszową. Dwaj gracze na zmianę przesuwają wspólny pionek wzdłuż narysowanych na planszy ścieżek. Gracz, który nie będzie mógł wykonać ruchu (pionek będzie już na mecie), przegrywa. Gdybyś był graczem zaczynającym rozgrywkę, jaki byłby Twój pierwszy ruch?
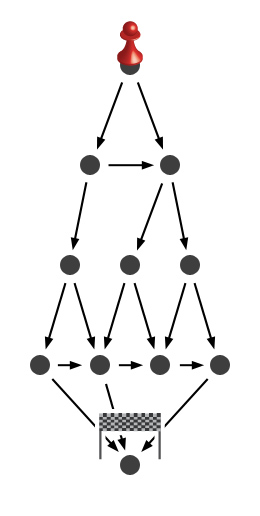
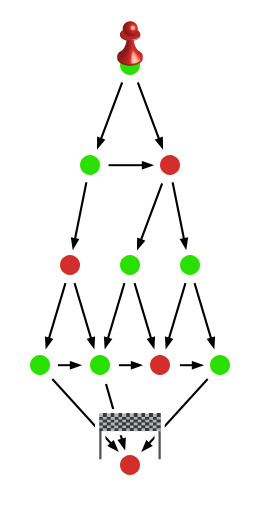
Plansza ma tylko kilka pól i niewiele więcej połączeń - cierpliwy Czytelnik może spróbować rozważyć wszystkie możliwe scenariusze rozgrywki. My zastosujemy nieco zmyślniejsze rozwiązanie. Przyjrzyjmy się planszy i spróbujmy na początek przypisać każdemu polu jedną z dwóch cech:
Nie jest intuicyjnie oczywiste, że każde pole będzie można tak zaklasyfikować. A jednak! Jeśli w naszym ruchu pionek znajduje się już na mecie, automatycznie przegrywamy. To pole jest więc łatwe do klasyfikacji - trudno o bardziej jaskrawy przykład pozycji przegrywającej. Spójrzmy teraz na pola, z których można w jednym ruchu przejść do mety. To doskonałe pozycje dla osoby, która wykonuje ruch - nic prostszego, niż przesunąć pionek na metę, wygrywając tym samym grę. Szybko udało nam się znaleźć jedną pozycję przegrywającą i kilka wygrywających. A co z pozostałymi polami?
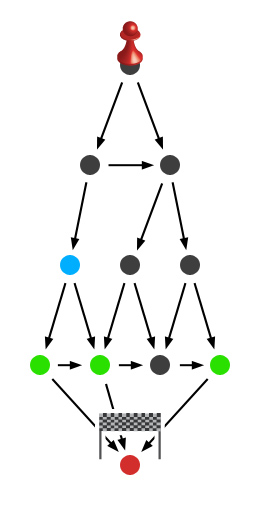
Na kolejnym rysunku kolorami zielonym i czerwonym zaznaczono pozycje, które już przeanalizowaliśmy. Teraz przyjrzymy się kolejnemu polu, zaznaczonemu na rysunku kolorem niebieskim. Wykonując ruch z tego pola, mamy do wyboru dwie drogi - obie prowadzą do pozycji, które zaklasyfikowaliśmy wcześniej jako wygrywające. Niezależnie od tego, którą drogę wybierzemy, po wykonaniu ruchu z niebieskiego pola, przeciwnik znajdzie się w pozycji wygrywającej (więc ostatecznie zwycięży). Nieuchronne zwycięstwo naszego oponenta oznacza - niestety - naszą nieuniknioną klęskę. Znaleźliśmy więc kolejną pozycję przegrywającą. Po przeprowadzeniu identycznego rozumowania dla jeszcze jednego pola, nasz szkic wygląda tak:
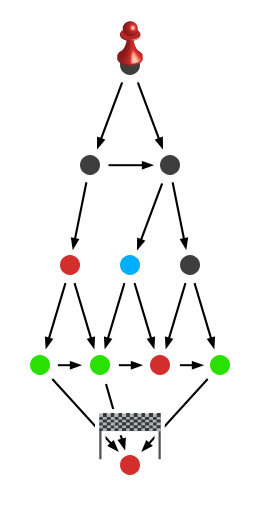
Z pola, które analizujemy w następnej kolejności (kolor niebieski) można wykonać dwa ruchy, jeden z nich prowadzi do pozycji wygrywającej, drugi - do przegrywającej. I właśnie istnienie tej jednej drogi wiodącej do pozycji przegrywającej jest kluczowe. Idąc tą ścieżką pozostawimy przeciwnika w pozycji gwarantującej ostateczną porażkę. Rozważane pole jest zatem pozycją wygrywającą. Warto podsumować wypracowaną właśnie metodę.
Zauważmy, że powyższe warunki są zupełne, tj. zawsze zachodzi jeden z nich. Wystarczy zaklasyfikować wszystkie następniki (pozycje, do których można dojść z danego pola), aby móc zaklasyfikować rozważane pole. Po zastosowaniu metody do pozostałych pól efekty analizy wyglądają następująco.
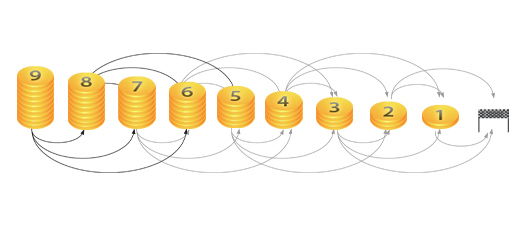
Czas zrobić z tych rozważań użytek. Wiemy już które pola są przegrywające, a które wygrywające. Jak za chwilę pokażemy, wiedza ta stanowi kompletną instrukcję prowadzącą do zwycięstwa zawodnika znajdującego się (tak jak my na początku gry) w pozycji wygrywającej! Skoro nasze pole jest wygrywające, to co najmniej jeden z możliwych ruchów prowadzi do pozycji przegrywającej - i to jest właśnie ruch, który każdorazowo warto wykonać. Wtedy przeciwnik będzie miał do wyboru tylko ruchy prowadzące do pozycji wygrywajacych. W ten sposób stale będziemy zaczynać ruch z pozycji wygrywającej, a nasz oponent - z przegrywającej. Gra musi się kiedyś skończyć (plansza nie ma cykli po których można by było krążyć), a rozumowanie z poprzedniego zdania gwarantuje, że na mecie bez możliwości ruchu zostanie pozostawiony nasz przeciwnik. Przedstawione postępowanie jest fundamentem analizy praktycznie wszystkich gier "matematycznych" z jakimi mamy do czynienia (przez grę matematyczną rozumiemy tutaj taką, która polega wyłącznie na podejmowaniu decyzji, a nie - na przykład - odbijaniu piłki przez siatkę). przyjrzyjmy się dla przykładu innej grze, tym razem bez planszy i pionka. Dwaj gracze siadają do stołu, na którym znajduje się stosik kilkunastu monet. Umawiają się, że na zmianę będą zdejmować z niego jedną, dwie lub trzy monety. Zwycięzcą będzie ten gracz, który w swoim ruchu zdejmie ostatnią monetę. Tak jak poprzednio, będziemy chcieli ocenić występujące w grze pozycje. Tym razem jednak nie ma jawnie określonej planszy, na której można by je było wskazać palcem. Musimy więc sami ją sobie wyobrazić. A właściwie jego, bo pod naszym słowem "plansza" kryje się pojęcie grafu gry, i tej nazwy będziemy odtąd używać. Rolę pola z gry planszowej pełni tym razem liczba pozostałych na stole monet. Brak monet na stole stanowi naszą "metę". Z pozycji, w której na stole pozostało N monet można przejść do pozycji N-1, N-2 oraz N-3.
Takie grafy gier potrafimy już analizować, pozostawiamy więc tę przyjemność Czytelnikowi - zdradzając tylko, że w występowaniu pozycji wygrywających i przegrywających powinno dać się zauważyć pewną regularność. Po nabraniu wprawy w rozpoznawaniu w grafie zwycięskich pozycji dojdziesz pewnie do słusznego wniosku, że jedyną trudnością bywa co najwyżej znalezienie grafu danej gry - reszta pracy jest już prosta. Tymczasem zbliżamy się do końca artykułu, czas więc na kilka podsumowań. Zaprezentowaliśmy Ci, Czytelniku, podstawy teorii gier. To bardzo szeroka dziedzina - my ograniczyliśmy się do tych gier, które da się opisać jak zbiór pozycji (pole na planszy, liczba monet na stole), połączonych dozwolonymi przez zasady ruchami (do jakich pozycji możemy przejść z danej). Poznaliśmy też pojęcie grafu gry, pozwalającego na czytelne przedstawienie spełniających te warunki gier. Wreszcie - nauczyliśmy się skutecznej metody ich analizowania i zastosowaliśmy ją w dwóch prostych przykładach. Prostych, bo w naszych grach mamy tylko dwóch graczy, rozgrywki zawsze kończą się w skończonej liczbie ruchów, a w dodatku każdy zawodnik w danej pozycji ma identyczny zestaw możliwych ruchów (zauważmy, że nie jest tak na przykład w szachach - przy danym układzie pionków gracz biały może przejść do zupełnie innych układów, niż gracz czarny). Kiedy któryś z tych warunków przestaje być spełniony, komplikują się też metody analizy. Jeśli więc zainteresowała Cię ta tematyka, nie musisz obawiać się nudy i szybkiego wyczerpania materiału do zgłębienia. Morał z tych opowieści płynie dwojaki:
Czego wszystkim czytelnikom Portalu życzę :). * 'Dżentelmen' - taki właśnie napis widnieje na nagrobku Williama Shakeapeare'a - autora przytoczonych słów.
(9 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com