Snakes on a plane
06.02.2009 - Tomasz Czajka
   W maju 2008 roku w Las Vegas odbyły się zawody TopCoder Open 2008. W eliminacjach online turnieju algorytmicznego wzięło udział ponad 1700 zawodników, z czego do finałów w Las Vegas zakwalifikowało się 72 osoby. Decydujące zadanie finału TopCoder Open 2008Półfinał i runda dogrywkowaPo trudnej walce w jednym z trzech 16-osobowych półfinałów nie udało mi się wprawdzie zająć miejsca w pierwszej trójce, które gwarantowałoby miejsce w wielkim finale, ale z siódmego miejsca awansowałem do dogrywki ostatniej szansy dla osób z miejsc 4-7. Całe szczęście, dogrywkę tę udało mi się wygrać, dzięki czemu wskoczyłem do finału jako ostatni, 10-ty zawodnik. FinałWidząc, że szczęście mi sprzyja, przyjąłem agresywną strategię w finale. Finał zawierał tradycyjnie 3 zadania, za które można było zdobyć maksymalnie 250, 500 i 1000 punktów. Na implementację rozwiązań przewidziano 85 minut czasu. Zwykle zawodnicy rozwiązują zadania w kolejności od najłatwiejszego do najtrudniejszego, i to była szansa dla mnie. Po uporaniu się z zadaniem za 250 w ciągu 23 minut, przeskoczyłem zadanie za 500 i otworzyłem zadanie za 1000, wiedząc, że jeśli w ciągu następnej godziny zaimplementuję poprawne rozwiązanie, da mi to spore szanse na zwycięstwo w turnieju (i $15000). Zgodnie z planem, okazało się, że wysłałem rozwiązanie zadania za 1000 jako jedyny. Dało mi to 696 punktów, i (jak mi się wydawało) bezpieczną odległość przed resztą zawodników. Za mną Petr Mitrichev z 558 punktami i Eryk Kopczyński z 557 punktami, obaj rozwiązali zadania za 250 i 500 (liczba punktów zależy również od czasu wysłania rozwiązania). Wydawało się, że wszystko zależy już tylko od tego, czy moje rozwiązania okażą się poprawne czy nie. Przed nami jednak jeszcze 10-minutowa sesja Challenge Phase, w której można zdobyć 50 punktów za znalezienie błędu w programie jednego z przeciwników. Stało się to, co wydawało mi się niemożliwe - Petr pokonał 3 inne programy, zdobywając tym 150 punktów i wyprzedzając mnie o 12 punkcików. 24 sekundy przed końcem. Ja do tej pory spokojnie przeglądałem rozwiązania innych, nie przewidując takiego scenariusza. Wolałem nie ryzykować ataku na czyjekolwiek rozwiązania, aby nie zmniejszyć dystansu. Z letargu obudziły mnie nagłe okrzyki publiczności, która widocznie śledziła pościg Petra z zapartym tchem. No cóż, zostały 24 sekundy. Otworzyłem jedno z rozwiązań zadania po 250, które wydawało mi się nieco zbyt skomplikowane. Nie mając wiele do stracenia, szybko wpisałem w okienko dwie liczby "0, 50" (prosty test poprawnościowy). O dziwo, program padł! "Segmentation fault" i znowu ja na prowadzeniu. Petr jeszcze walczył do końca i zdążył wysłać jeszcze jeden test 2 sekundy przed końcem. Na moje szczęście, zaatakował poprawny program, i ta dramatyczna walka zakończyła się moim zwycięstwem. Zadanie za 1000Odstawiając na bok tę strzelaninę z ostatnich sekund, przejdźmy teraz do samego zadania za 1000 pkt. Nazywało się ono "Snakes on a plane", oryginalną treść można przeczytać po zalogowaniu się na stronie TopCodera. Zadanie ma dosyć prostą treść. Jednak moje rozwiązanie było zupełnie inne od podejścia, którego spodziewali się autorzy zadania. Zadanie sprowadza się do następującego problemu. Mamy daną szachownicę o wielkości nie większej niż 12 x 12, z której wycięte są pewne pola. Należy pokryć pozostałe pola wężami, przy czym dostępne są dwa rodzaje węży:
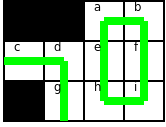
Zadanie polega na tym, żeby takimi wężami pokryć wszystkie niewycięte pola, przy czym należy użyć jak najmniejszej liczby węży-linii. Liczba węży-pętli nie ma znaczenia. Na wyjściu należy podać liczbę potrzebnych węży-linii, lub powiedzieć że nie da się pokryć wszystkich pól. Oto przykładowe rozwiązanie.
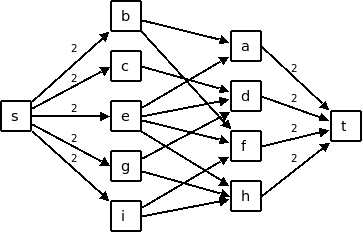
Czarne pola są wycięte. Użyliśmy jednego węża-pętli oraz jednego węża-linii. Odpowiedź w tym przypadku to 1. Jak znaleźć optymalne rozwiązanie? Zignorujmy na początek węże-linie i skupmy na pytaniu - czy można szachownicę pokryć samymi wężami-pętlami? Kluczowe jest następujące spostrzeżenie: w pokryciu wężami-pętlami, każde pole połączone jest z dokładnie dwoma sąsiednimi polami. Co więcej, jeśli uda nam się tak połączyć pary sąsiednich pól, aby każde było połączone z dokładnie dwoma sąsiednimi polami, to otrzymamy pokrycie wężami-pętlami. Zatem musimy sprawdzić, czy da się wykonać takie połączenie. Jest to prawie dokładnie klasyczne pytanie o istnienie skojarzenia doskonałego w grafie. Z tym, że w naszym przypadku każdy wierzchołek grafu chcemy połączyć nie z jednym, a z dwoma sąsiadami. Nasz graf jest dwudzielny (czarne pola zawsze sąsiadują z białymi na normalnie pokolorowanej szachownicy), więc możemy zastosować standardowy algorytm wykorzystujący algorytm znajdowania maksymalnego przepływu w grafie. Dzielimy wierzchołki na dwie grupy: "czarne" i "białe". W naszym przypadku czarne to b, c, e, g, i, a białe to a, d, f, h. Łączymy sąsiednie wierzchołki krawędziami. Dodajemy dwa wierzchołki: "źródło" s oraz "ujście" t. Łączymy źródło ze wszystkimi "czarnymi" wierzchołkami, a ujście ze wszystkimi "białymi" (przy czym krawędziom tym nadajemy przepustowość 2). Oto nasz graf:
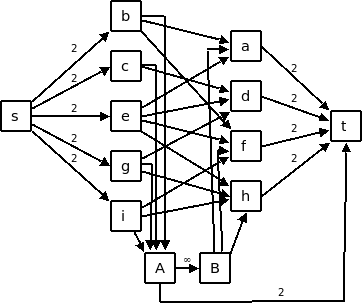
Możemy przekonać się, że naszego doskonałego skojarzenia można dokonać wtedy i tylko wtedy, gdy w tak wygenerowanym grafie istnieje przepływ, który nasyca wszystkie krawędzie wychodzące ze źródła oraz wszystkie wpadające do ujścia. W naszym przypadku, takie skojarzenie nie jest możliwe - choćby z tej przyczyny, że liczba czarnych i białych wierzchołków jest różna. Wynika z tego, że nie wystarczą tu węże-pętle. Potrzebny jest co najmniej jeden wąż-linia. Możemy teraz zauważyć, że węże-linie możemy obsłużyć w prawie ten sam sposób. Różnią się one jedynie tym, że ich końce na brzegu planszy mają nie dwóch, a jednego sąsiada. Dostawmy więc dwa "wirtualne" wierzchołki reprezentujące połączenia ze ścianą, A i B. A służy jako sąsiad dla czarnych brzegowych wierzchołków, B dla białych. Otrzymujemy następujący graf:
Ponieważ czarnych wierzchołków jest o 1 więcej niż białych, i każdy ma 2 połączenia, co najmniej 2 czarne wierzchołki muszą być połączone ze ścianą. Dokładniej, liczba czarnych wierzchołków połączonych ze ścianą będzie dokładnie o 2 większa od liczby białych wierzchołków połączonych ze ścianą. Zatem, liczba połączeń wpływających do A będzie dokładnie o 2 większa, niż tych wypływających z B. Co najmniej 2 czarne wierzchołki muszą być połączone ze ścianą. Dodaliśmy zatem krawędź od A do t o przepustowości 2. Może jednak okazać się, że więcej niż 2 czarne wierzchołki będą połączone ze ścianą. Powiedzmy, że jest ich 5. Wtedy dokładnie 3 białe wierzchołki muszą być połączone ze ścianą, dla równowagi. W naszym grafie, A będzie połączone z pięcioma wierzchołkami, a B z trzema. W takim wypadku mielibyśmy razem 8 wierzchołków połączonych ze ścianami, czyli 4 węże-linie. Aby umożliwić takie rozwiązania, dodajmy dodatkową krawędź od A do B o nieskończonej przepustowości. "Nadmiar" czarnych wierzchołków połączonych ze ścianą, czyli w naszym grafie przepływ wpływający do A, przepływa do B, co umożliwia połączenie tej samej liczby nadmiarowych białych wierzchołków ze ścianą. Nasze zadanie polega teraz na znalezieniu pełnego przepływu, który używa jak najmniejszej przepustowości z A do B. Im mniejszy przepływ od A do B, tym mniej wierzchołków połączonych ze ścianą, czyli tym mniej węży-linii. Jak możemy znaleźć taki przepływ? Można to rozwiązać na kilka sposobów. Ja użyłem następującego. Zaczynamy od przepustowości 0 na krawędzi A-B i znajdujemy maksymalny przepływ. Jeśli jest on "pełny" to znaleźliśmy rozwiązanie. Jeśli nie, to zwiększamy przepustowość tej krawędzi o 1 i próbujemy poprawić przepływ, używając metody ścieżki powiększającej Forda-Fulkersona. Proces ten powtarzamy do momentu, aż znajdziemy pełny przepływ (co daje nam rozwiązanie) lub gdy powiększanie przepustowości nie poprawia przepływu. W tym drugim przypadku rozwiązanie nie istnieje. (12 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com