Crazy painter
04.02.2009 - Marek Cygan
  Zadanie polega na jak najszybszym pomalowaniu prostokątnej planszy o m wierszach oraz n kolumnach. Dla każdego z mn pól planszy znany jest kolor, na który trzeba to pole pomalować. Pola mogą być malowane wielokrotnie, przy czym dane pole za każdym razem musi być malowane tym samym kolorem (docelowym). Do malowania możemy wykorzystać następujące operacje:
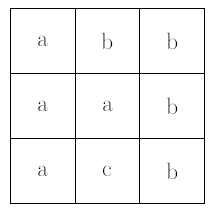
Zauważmy, że czas malowania zarówno paska poziomego jak i pionowego nie zależy od ich długości. Jeśli zatem zdecydujemy się pomalować poziomy pas pól, to możemy go przedłużyć w lewo oraz w prawo do paska maksymalnego, czyli do momentu w którym trafimy na brzeg planszy lub pole innego koloru. Analogicznie paski pionowe opłaca się maksymalnie przedłużyć w górę oraz w dół. Całą planszę możemy zatem podzielić na maksymalne paski poziome, gdzie każde pole planszy będzie należało do dokładnie jednego paska. Podobnie planszę możemy również podzielić na maksymalne paski pionowe. Załóżmy, że do pomalowania mamy następującą planszę:
Podział powyższej planszy na maksymalne paski poziome i pionowe będzie wyglądał następująco (każdy maksymalny pasek został oznaczony innym kolorem):
Nietrudno zauważyć, że kolejność operacji, które będziemy wykonywać nie ma znaczenia, gdyż nie wolno nam malować dwa razy tego samego pola na różne kolory. Możemy zatem wywnioskować, że cała plansza zostanie pomalowana wtedy i tylko wtedy, gdy dla każdego pola co najmniej jedna z następujących operacji zostanie wykonana:
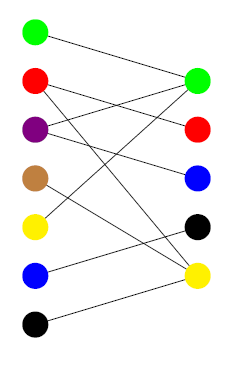
Chcielibyśmy zbudować obiekt kombinatoryczny, który będzie posiadał właściwość analogiczną do powyższej obserwacji. W tym celu skonstruujmy graf dwudzielny, którego wierzchołkami będą maksymalne paski pionowe oraz poziome. Dwa paski połączone będą krawędzią wtedy i tylko wtedy gdy mają one wspólne pole, zatem liczba krawędzi w naszym grafie będzie równa liczbie pól na planszy - mn. Warto zapamiętać ten pomysł: bardzo często wyobrażenie sobie planszy jako grafu dwudzielnego, w którym każda krawędź odpowiada pojedynczej komórce, ułatwia znalezienie rozwiązania. Dla naszej przykładowej planszy graf będzie wyglądał następująco (po lewej stronie znajdują się wierzchołki odpowiadające paskom poziomym).
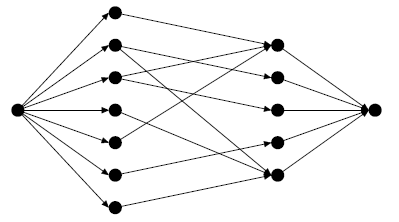
Do naszego grafu dodamy jeszcze dwa specjalne wierzchołki, które będziemy nazywać źródłem oraz ujściem. Źródło połączymy ze wszystkimi wierzchołkami lewej warstwy, natomiast od każdego wierzchołka prawej warstwy poprowadzimy krawędź do ujścia.
Masz prawo zastanawiać się w tej chwili Drogi Czytelniku po co nam ten graf i jakie są jego własności. Otóż każdą z operacji malowania możemy utożsamić z krawędzią tego grafu. Krawędzie łączące źródło z wierzchołkami lewej warstwy odpowiadają malowaniu pasków poziomych. Krawędzie pomiędzy warstwami odpowiadają pomalowaniu pojedynczych pól, natomiast krawędzie prowadzące od wierzchołków prawej warstwy do ujścia to operacje malowania pasków pionowych. Wciąż nasuwa się jednak pytanie: cóż z tego? Odpowiedzią jest ostatnia już, aczkolwiek najważniejsza obserwacja. Podzbiór zbioru krawędzi naszego grafu jest rozwiązaniem - odpowiada pomalowaniu całej planszy - wtedy i tylko wtedy, gdy po usunięciu krawędzi z tego zbioru nie istnieje ścieżka od źródła do ujścia. Dowód: Wystarczy zauważyć, że każda ścieżka od źródła do ujścia składa się z dokładnie trzech krawędzi, które odpowiadają trzem sposobom, na jakie możemy pomalować dane pole, jeśli ścieżka ta przetrwa po usunięciu krawędzi, których użyliśmy jako operacji malowania, to znaczy, że nie wykonaliśmy żadnej z trzech operacji powodujących pomalowanie danego pola, co oznacza, że pole to pozostanie niepomalowane. Jeśli zatem krawędziom przypiszemy koszty odpowiadające czasom wykonania danych operacji, to minimalny przekrój w naszym grafie jest poszukiwanym przez nas rozwiązaniem zadania! Przekrój taki możemy znaleźć w czasie O(w3) używając klasycznych algorytmów, gdzie w to liczba wierzchołków naszego grafu, czyli w=O(nm). (6 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com