Password suspects
03.08.2009 - Alan Meller
  Jednym z moich ulubionych zadań algorytmicznych jest Password Suspects z ACM World Finals 2008. Kapitan naszej drużyny przydzielił mi je wtedy mówiąc, że „to chyba jest dość proste”. Po dokładnym przeczytaniu treści tego oraz innych zadań, które miałem rozwiązać tamtego dnia uznałem, że to jednak nie jest zupełnie trywialne i póki co zajmę się innym, prostszym. Niestety, początek tego konkursu był dla nas nieudany i po około półtorej godziny zaczęliśmy być już mocno z tyłu. Jednocześnie stało się jasne, że jest to zadanie z kategorii tych, które trzeba zrobić by móc liczyć na dobry wynik i że jeśli uda nam się rozwiązać je szybko, będziemy mieli szansę nie stracić kontaktu z czołówką. Zapamiętałem to zadanie właśnie z powodu emocji, które towarzyszyły mi przy jego rozwiązywaniu. Poza tym okazało się ono dosyć oryginalne o tyle, że wymagało zastosowania dwóch różnych kategorii algorytmów. Tego typu zadania nie zdarzają się często i prawie zawsze stanowią ciekawe wyzwanie. ZadanieOryginalną treść zadania można znaleźć tutaj, a jej skrócona wersja wyląda tak: Dane jest
Jeśli takich słów jest co najwyżej 42, należy dodatkowo je wszystkie wypisać. Ograniczenia:
Przykładowo, dla Pierwszy pomysłKrótka analiza zadania doprowadziła mnie do kilku wniosków. Po pierwsze, z całą pewnością nie jest to trywialne zadanie, które można rozwiązać w sposób zupełnie brutalny – wszystkich możliwych słów do sprawdzenia jest potencjalnie Wróciłem więc do analizy zadania, a dokładniej przemyślałem warunki narzucone na słowa, które trzeba zliczyć. Dwa pierwsze wyglądały na proste i naturalne, niestety jednak wszystko komplikował warunek trzeci, tj. zawieranie każdego z danych M wzorców jako spójnego podsłowa. Po sprawdzeniu kilku naiwnych podejść okazało się, że nie jest to proste. Chociażby dlatego, że niektóre spośród tych wzorców mogą mieć wspólne fragmenty, czy wręcz się w sobie zawierać. Ponadto, dopuszczalne są również słowa, w których jakiś z wzorców występuje kilka razy. Tak czy inaczej dość szybko zdałem sobie sprawę, że próby prostego zliczania szukanych słów nie mają szansy powodzenia. Na szczęście wtedy przyjrzałem się dokładniej ograniczeniom danych. Czasami naprawdę warto to zrobić!. Cóż, z praktyki wynika, że w tego typu zadaniach jednym z parametrów przy programowaniu dynamicznym jest długość zliczanych słów. Zazwyczaj okazuje się, że mając wyliczone „pewne informacje” dla wszystkich słów o długości Jeden wzorzecMając w pamięci fakt, że muszę uporać się przede wszystkim z warunkiem trzecim (o wzorcach jako podsłowach) zabrałem się w końcu za ten problem. Pomocnicze pytanie, które można zadać sobie w takiej sytuacji to: „A jak można by to rozwiązać, gdyby był tylko jeden wzorzec?”. Dłuższa chwila zastanowienia i ten uproszczony przypadek okazuje się nie być aż tak trudny. Załóżmy, że wiem ile jest słów długości
Przypadek 1) jest prosty. Do każdego słowa zawierającego wzorzec mogę dopisać na końcu dowolną literę i dalej będzie ono zawierać ten wzorzec. Ponieważ jest tylko Nieco trudniejszy jest przypadek 0). Załóżmy, że mamy słowo, które nie zawiera wzorca, ale jego ostatnich Całe rozumowanie ilustruje następujący (pseudo)kod:
W liniach (1)-(3) zeruję tablicę do której będę dodawał znalezione słowa długości Wracamy do oryginalnej wersjiUmiem więc już rozwiązać prostszą wersję zadania, taką, gdzie jest tylko jeden wzorzec. Spróbuję więc uogólnić to rozumowanie tak, by było ono w stanie obsłużyć nie jeden, lecz
Punkt a) okazuje się być dość prosty. To, które wzorce wystąpiły w tekście, można pamiętać w masce bitowej, tj. w liczbie składającej się z Punkt b) jest trochę bardziej skomplikowany. Idealnym rozwiązaniem jest użycie w tym celu automatu Aho – Corasick. Automat ten jest w pewnym sensie uogólnieniem tablicy prefiksowej użytej w prostszym wariancie zadania, czyli właśnie tym, czego mi potrzeba. Mając zbudowaną tą strukturę dla podanych wzorców, można w algorytmie dynamicznym zamiast ilości ostatnich liter słowa zgodnych z wzorcem pamiętać numer stanu automatu. Wyznaczenie stanu po dodaniu litery jest jeszcze prostsze niż dla tablicy prefiksowej, gdyż wystarczy skorzystać z funkcji przejścia automatu. Ogólnie rozwiązanie korzystające z automatu Aho – Corasick jest w tym zadaniu bardzo eleganckie i zdecydowanie je polecam. Niestety jednak, szczegóły tej struktury wykraczają poza zakres artykułu. Chętni na pewno znajdą wystarczająco dużo materiałów na ten temat w internecie. Niemniej jednak można uporać się z punktem b) również w mniej elegancki sposób. Można na przykład pamiętać ilość liter zgodnych z ostatnimi literami słowa dla każdego wzorca z osobna. Wszystkich możliwości jest co prawda za dużo by pamiętać to w zupełnie brutalny sposób (nawet Koniec?Niestety, historia tego zadania nie ma szczęśliwego zakończenia. Pomimo usilnych starań nie udało się nam rozwiązać go w trakcie trwania zawodów. Nie zmienia to jednak faktu, że zadanie to szczególnie podoba mi się za to, że w interesujący sposób łączy w sobie programowanie dynamiczne z zaawansowanym algorytmem tekstowym. Uważam je również za okazję do ciekawej rozrywki i do nauczenia się czegoś nowego – i przede wszystkim tego życzę wszystkim Czytelnikom :) (2 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


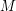 wzorców oraz pewna liczba naturalna
wzorców oraz pewna liczba naturalna 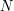 . Oblicz, ile jest słów, które jednocześnie
. Oblicz, ile jest słów, które jednocześnie
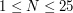
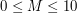
 do
do 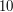 znaków i składa się wyłącznie z liter a-z.
znaków i składa się wyłącznie z liter a-z.
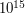 .
.
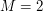 ,
, 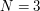 i danych wzorców „ab”, „ba” dopuszczalne są tylko 2 słowa: aba i bab.
i danych wzorców „ab”, „ba” dopuszczalne są tylko 2 słowa: aba i bab.
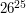 , czyli o wiele za dużo. Będzie trzeba więc skorzystać z jakiegoś sensownego algorytmu. Po drugie, dość intuicyjne wydało mi się przyjęcie, że największym problemem będzie tu samo policzenie ilości dopuszczalnych słów i póki co skupienie się jedynie na tym aspekcie zadania. Przypadek, gdy takich słów jest mało (co najwyżej 42) i trzeba je wszystkie wyznaczyć, wyglądał jedynie na dodatek, który miał umilić mi życie.
, czyli o wiele za dużo. Będzie trzeba więc skorzystać z jakiegoś sensownego algorytmu. Po drugie, dość intuicyjne wydało mi się przyjęcie, że największym problemem będzie tu samo policzenie ilości dopuszczalnych słów i póki co skupienie się jedynie na tym aspekcie zadania. Przypadek, gdy takich słów jest mało (co najwyżej 42) i trzeba je wszystkie wyznaczyć, wyglądał jedynie na dodatek, który miał umilić mi życie.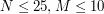 , każdy z wzorców ma długość co najwyżej
, każdy z wzorców ma długość co najwyżej  i krótszych, można dość łatwo wyliczyć te same informacje dla słów długości
i krótszych, można dość łatwo wyliczyć te same informacje dla słów długości 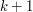 . Powtarzając ten krok odpowiednią ilość razy otrzymamy w końcu wynik dla słów o długości zadanej w treści zadania. Trudność polega tutaj jednak na określeniu co to są te „pewne informacje”. Intuicyjnie, chciałbym znaleźć takie parametry dla programowania dynamicznego (poza długością słowa), które mając wyznaczone dla słów krótszych, będę umiał wyznaczyć dla słów dłuższych. No i chcę, żeby tych parametrów było jak najmniej, tak, aby móc zmieścić się w limitach pamięciowych i czasowych.
. Powtarzając ten krok odpowiednią ilość razy otrzymamy w końcu wynik dla słów o długości zadanej w treści zadania. Trudność polega tutaj jednak na określeniu co to są te „pewne informacje”. Intuicyjnie, chciałbym znaleźć takie parametry dla programowania dynamicznego (poza długością słowa), które mając wyznaczone dla słów krótszych, będę umiał wyznaczyć dla słów dłuższych. No i chcę, żeby tych parametrów było jak najmniej, tak, aby móc zmieścić się w limitach pamięciowych i czasowych.![$ dp[k][0][p] $](/files/tex/b0e56f7badba08d18bdab737e86038e8c2acc9cc.png)
![$ dp[k][1] $](/files/tex/73b28f0dc7e3e92dac1eae4ea645c8f5a8f44749.png)
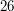 angielskich liter (czytelnik może to policzyć używając swoich palców u rąk, u nóg i palców u rąk koleżanki) to mamy znalezionych już
angielskich liter (czytelnik może to policzyć używając swoich palców u rąk, u nóg i palców u rąk koleżanki) to mamy znalezionych już ![$ 26*dp[k][1] $](/files/tex/5d72619300d71b72640ac8481a2b6e1fc53e6ed9.png) słów zawierających wzorzec o długości
słów zawierających wzorzec o długości  liter jest zgodne z
liter jest zgodne z  , ale oczywiście rozumowanie przebiega identycznie dla każdej wartości
, ale oczywiście rozumowanie przebiega identycznie dla każdej wartości 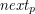 . Dzięki niej mamy znalezionych
. Dzięki niej mamy znalezionych ![$ dp[N][1] $](/files/tex/0db28f5c17c65b46e6648bda380577cf5c8146fb.png) . Przypadek, gdy liczba ta jest mała i trzeba wypisać wszystkie znalezione słowa jest standardowym „dodatkiem” do algorytmu dynamicznego. Uporanie się z nim nie jest trudne i pozostawię to jako ćwiczenie Czytelnikowi.
. Przypadek, gdy liczba ta jest mała i trzeba wypisać wszystkie znalezione słowa jest standardowym „dodatkiem” do algorytmu dynamicznego. Uporanie się z nim nie jest trudne i pozostawię to jako ćwiczenie Czytelnikowi.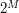 różnych wartości. W tym zadaniu jednak
różnych wartości. W tym zadaniu jednak 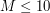 , więc
, więc 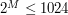 – dostatecznie mało, by rozwiązanie korzystające z takiego pomysłu okazało się sensowne (a przynajmniej nie wydawało się całkiem bezużyteczne).
– dostatecznie mało, by rozwiązanie korzystające z takiego pomysłu okazało się sensowne (a przynajmniej nie wydawało się całkiem bezużyteczne).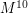 !), jednak łatwo przekonać się, że zdecydowana większość z nich nie może nigdy zajść. W praktyce, można pamiętać wszystkie sensowne możliwości np. korzystając ze struktury mapy, dostępnej w bibilotece stl w c++ i w java.utils w javie. Można również pamiętać dla którego wzorca zgodnych jest najwięcej liter oraz ilość liter zgodnych z tym wzorcem. Dla tych rozwiązań szczegóły implementacyjne są dość skomplikowane, więc nie będę się nad nimi rozwodził. Dla chętnych czytelników wgłębienie się w nie może jednak być dobrym ćwiczeniem.
!), jednak łatwo przekonać się, że zdecydowana większość z nich nie może nigdy zajść. W praktyce, można pamiętać wszystkie sensowne możliwości np. korzystając ze struktury mapy, dostępnej w bibilotece stl w c++ i w java.utils w javie. Można również pamiętać dla którego wzorca zgodnych jest najwięcej liter oraz ilość liter zgodnych z tym wzorcem. Dla tych rozwiązań szczegóły implementacyjne są dość skomplikowane, więc nie będę się nad nimi rozwodził. Dla chętnych czytelników wgłębienie się w nie może jednak być dobrym ćwiczeniem.

