Zanim przejdziemy do treści i opisu rozwiązania, kilka informacji o zadaniu. Możecie je znaleźć na SPOJu (tutaj), umieścił je tam Qu Jun, ale nie jestem pewien, czy to on jest jego autorem. Niektórzy pewnie zauważyli dziwny pogrubiony napis na dole strony, w pewnym sensie to ja jestem jego sprawcą. Zadanie to udało mi się zaakceptować dopiero za 23 razem, wynikało to głównie z drobnych błędów implementacyjnych (nie należy się tym przerażać, pewnie większości z Was uda się dużo szybciej!), a po drodze spowodowałem chyba 3-krotne ponowne sprawdzenie rozwiązań - wysłałem, przeszło, poszedłem spać, rano wstaję i widzę WA... Mój program nie jest najszybszy, wierzę, że istnieje lepszy (w sensie złożoności), ale również może być tak, że po prostu moja implementacja nie jest zoptymalizowana. Jednak nawet jeżeli już wpadliście na wydajne rozwiązanie polecam doczytać do końca, znajdziecie tutaj jedną naprawdę fajną sztuczkę.
Treść
Dane jest drzewo o N wierzchołkach, które oznaczamy liczbami 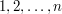 . Każda z jego
. Każda z jego 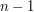 krawędzi ma przyporządkowaną całkowitoliczbową wagę (być może ujemną). Dodatkowo każdy wierzchołek jest pomalowany na czarno lub biało. Na samym początku wszystkie wierzchołki są białe. Niech
krawędzi ma przyporządkowaną całkowitoliczbową wagę (być może ujemną). Dodatkowo każdy wierzchołek jest pomalowany na czarno lub biało. Na samym początku wszystkie wierzchołki są białe. Niech 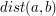 oznacza wagę (jedynej) ścieżki między wierzchołkiem
oznacza wagę (jedynej) ścieżki między wierzchołkiem  i
i  . Naszym celem jest (wydajne!) przetworzenie ciągu
. Naszym celem jest (wydajne!) przetworzenie ciągu 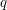 operacji, z których każda to
operacji, z których każda to
-
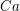 , zmień kolor wierzchołka
, zmień kolor wierzchołka  na przeciwny,
na przeciwny,
lub
-
 , oblicz wagę najcięższej ścieżki między (dowolnymi) dwoma białymi wierzchołkami.
, oblicz wagę najcięższej ścieżki między (dowolnymi) dwoma białymi wierzchołkami.
Wierzchołków oraz operacji jest co najwyżej 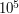 , wagi krawędzi należą do zakresu
, wagi krawędzi należą do zakresu ![$ [-1000 .. 1000] $](/files/tex/a7415aee109b1b01269b33e3f62897a7d097e407.png) .
.
Rozwiązanie nieoptymalne
Atak na problem rozpoczniemy od powszechnej praktyki - uproszczenia problemu. Warto zawsze zaczynać właśnie od tego, często właśnie tak można zbliżyć się do prawidłowego rozwiązania. Pamiętajcie, że autorzy zadania to też ludzie, którzy często podczas układania zadań stosują strategię "wymyśl problem, a potem postaraj się go maksymalnie utrudnić". W tym konkretnym wypadku warto na początek założyć, że każdy wierzchołek ma jakiś kolor (niekoniecznie wszystkie taki sam), a jedyną operacją, którą chcemy wykonać (tylko raz), jest  . Łatwo zauważyć, że w takim wypadku algorytm musi działać w czasie
. Łatwo zauważyć, że w takim wypadku algorytm musi działać w czasie 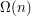 : trzeba popatrzeć przynajmniej raz na każdy wierzchołek. A czy istnieje algorytm, który działa dokładnie w takim czasie? Tak! Z pomocą przychodzi nam tutaj programowanie dynamiczne (czy też, dla tych z Was, którzy czują się bardziej matematykami, rozumowanie indukcyjne). Bazą indukcji jest drzewo składające się z jednego wierzchołka, dla którego bez problemu możemy obliczyć odpowiedź. W kroku indukcyjnym mamy całe, być może bardzo duże, drzewo. Wybierzmy jeden z wierzchołków
: trzeba popatrzeć przynajmniej raz na każdy wierzchołek. A czy istnieje algorytm, który działa dokładnie w takim czasie? Tak! Z pomocą przychodzi nam tutaj programowanie dynamiczne (czy też, dla tych z Was, którzy czują się bardziej matematykami, rozumowanie indukcyjne). Bazą indukcji jest drzewo składające się z jednego wierzchołka, dla którego bez problemu możemy obliczyć odpowiedź. W kroku indukcyjnym mamy całe, być może bardzo duże, drzewo. Wybierzmy jeden z wierzchołków  i ukorzeńmy w nim drzewo. Powiedzmy, że
i ukorzeńmy w nim drzewo. Powiedzmy, że  ma synów
ma synów 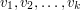 (
(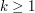 ). Możliwe są trzy sytuacje:
). Możliwe są trzy sytuacje:
- Szukana ścieżka przechodzi przez
 . Możemy ją wtedy podzielić na dwie części:
. Możemy ją wtedy podzielić na dwie części: 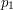 zawartą w podrzewie
zawartą w podrzewie 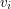 i
i 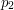 znajdującą się w poddrzewie
znajdującą się w poddrzewie 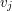 (
(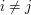 ). Każda z tych dwóch części jest najcięższą ścieżką zaczynającą się w białym wierzchołku i kończącą się w
). Każda z tych dwóch części jest najcięższą ścieżką zaczynającą się w białym wierzchołku i kończącą się w  w swoim poddrzewie.
w swoim poddrzewie.
- Szukana ścieżka kończy się w
 . Wtedy tak naprawdę jest ona najcięższą ścieżką zaczynającą się w białym wierzchołku i kończącą się w
. Wtedy tak naprawdę jest ona najcięższą ścieżką zaczynającą się w białym wierzchołku i kończącą się w  .
.
- Szukana ścieżka nie ma nic wspólnego z
 . Wtedy musi być całkowicie zawarta w poddrzewie wyznaczonym przez jednego z synów
. Wtedy musi być całkowicie zawarta w poddrzewie wyznaczonym przez jednego z synów  , czyli możemy zastosować rekurencyjnie (czy też indukcyjnie) to samo rozumowanie.
, czyli możemy zastosować rekurencyjnie (czy też indukcyjnie) to samo rozumowanie.
Wykorzystując te obserwacje łatwo jest stworzyć liniowe rozwiązanie bazujące na przeglądaniu w głąb. Wystarczy tylko w dowolny sposób ukorzenić całe drzewo, a następnie wyznaczać dla coraz większych poddrzew najcięższe ścieżki zaczynające się w białym wierzchołku i kończące się w korzeniu danego poddrzewa. Niech takie rozwiązanie nazywa się 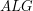 .
.
Trochę trudniej (ale dalej łatwo) zauważyć, że tak naprawdę to całe rozumowanie można zastosować do oryginalnego problemu, otrzymując rozwiązanie działające w czasie 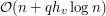 , gdzie
, gdzie 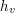 to wysokość drzewa zakorzenionego w (dowolnie wybranym) wierzchołku
to wysokość drzewa zakorzenionego w (dowolnie wybranym) wierzchołku  . Jak? Na pierwsze pytanie możemy odpowiedzieć używając
. Jak? Na pierwsze pytanie możemy odpowiedzieć używając 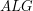 . Następnie zmieniamy kolor jednego wierzchołka
. Następnie zmieniamy kolor jednego wierzchołka  i zastanawiamy się, na jakie wartości wyznaczane w
i zastanawiamy się, na jakie wartości wyznaczane w 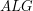 może wpłynąć taka zmiana? Okazuje się, że zmieniają się tylko wartości wyliczane na ścieżce z
może wpłynąć taka zmiana? Okazuje się, że zmieniają się tylko wartości wyliczane na ścieżce z  do korzenia
do korzenia  (której długość nie przekracza
(której długość nie przekracza 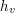 ). No dobrze, a skąd wziął się ten
). No dobrze, a skąd wziął się ten 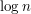 ? Uaktualniając wartości na ścieżce musimy wyznaczać nowe maksima (to jest najcięższe ścieżki zaczynająca się w białym wierzchołku i kończące się w korzeniu danego poddrzewo i najcięższa ścieżka w całym poddrzewie). Możemy albo za każdym razem przeglądać wszystkich synów danego wierzchołka na ścieżce (co nie jest najlepszym pomysłem), albo pamiętać te wartości w kolejce priorytetowej lub multisecie.
? Uaktualniając wartości na ścieżce musimy wyznaczać nowe maksima (to jest najcięższe ścieżki zaczynająca się w białym wierzchołku i kończące się w korzeniu danego poddrzewo i najcięższa ścieżka w całym poddrzewie). Możemy albo za każdym razem przeglądać wszystkich synów danego wierzchołka na ścieżce (co nie jest najlepszym pomysłem), albo pamiętać te wartości w kolejce priorytetowej lub multisecie.
By otrzymać z tego pomysłu wydajny algorytm wypadałoby znaleźć taki wierzchołek  , że
, że 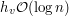 . Czasami jest to łatwe (na przykład w pełnym drzewie binarnym), a czasami niemożliwe... Zatem trafiliśmy w ślepą uliczkę? Nic bardziej mylnego!
. Czasami jest to łatwe (na przykład w pełnym drzewie binarnym), a czasami niemożliwe... Zatem trafiliśmy w ślepą uliczkę? Nic bardziej mylnego!
Fajny wierzchołek
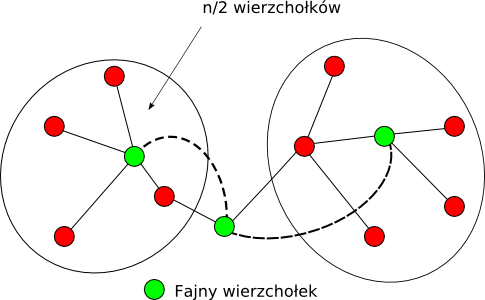
Na chwile odpłyniemy od naszego problemu. Okazuje się, że drzewa posiadają jedną ciekawą własność:
Niech  będzie dowolnym drzewem o
będzie dowolnym drzewem o  wierzchołkach. Istnieje taki wierzchołek
wierzchołkach. Istnieje taki wierzchołek 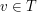 , że każda spójna składowa w
, że każda spójna składowa w 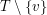 ma rozmiar nie większy niż
ma rozmiar nie większy niż 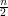 .
Jak się o tym przekonać? Niech
.
Jak się o tym przekonać? Niech  będzie na początku dowolnym wierzchołkiem. Jeżeli nie spełnia on powyższej tezy, ma dokładnie jednego sąsiada
będzie na początku dowolnym wierzchołkiem. Jeżeli nie spełnia on powyższej tezy, ma dokładnie jednego sąsiada  , który należy w
, który należy w 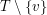 do spójnej składowej o rozmiarze przekraczającym
do spójnej składowej o rozmiarze przekraczającym 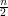 . W takim przypadku ustalamy
. W takim przypadku ustalamy  i powtarzamy całe rozumowanie. Czy takie postępowanie musi się kiedyś skończyć? Czy też może się zdarzyć, że wpadniemy w cykl? Niech
i powtarzamy całe rozumowanie. Czy takie postępowanie musi się kiedyś skończyć? Czy też może się zdarzyć, że wpadniemy w cykl? Niech 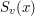 oznacza rozmiar składowej wierzchołka
oznacza rozmiar składowej wierzchołka  w
w 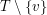 . Wtedy
. Wtedy
Reszta spójnych składowych dla

ma oczywiście rozmiar mniejszy niż
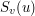
. Stąd rozmiar największej spójnej składowej cały czas się zmniejsza, zatem nasz proces musi się prędzej lub później skończyć.
No dobrze, ale właściwie po co to wszystko?
Algorytm
Skoro nie umiemy szybko wyliczać odpowiedzi w oryginalnym drzewie  , zmieńmy je na inne! Ale jak?... Warto, by miało jakiś korzeń, więc powiedzmy, że tym korzeniem będzie Fajny Wierzchołek dla
, zmieńmy je na inne! Ale jak?... Warto, by miało jakiś korzeń, więc powiedzmy, że tym korzeniem będzie Fajny Wierzchołek dla  . Analogicznie, synami korzenia będą Fajne Wierzchołki dla powstałych spójnych składowych. Powtarzamy to rozumowanie tak długo, jak składowe mają więcej niż jeden wierzchołek (czyli tak długo, jak można je dzielić). Dla wygody oznaczmy powstałe drzewo jako
. Analogicznie, synami korzenia będą Fajne Wierzchołki dla powstałych spójnych składowych. Powtarzamy to rozumowanie tak długo, jak składowe mają więcej niż jeden wierzchołek (czyli tak długo, jak można je dzielić). Dla wygody oznaczmy powstałe drzewo jako 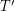 .
.
Łatwo zauważyć, że 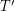 ma wysokość
ma wysokość 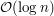 . Dlaczego? Każda ścieżka odpowiada w nim ciągowi coraz mniejszych spójnych składowych, z których każde dwie kolejne zawierają się w sobie, a co więcej rozmiar mniejszej nie przekracza połowy rozmiaru większej. Zauważmy też, że całe rozumowanie dotyczące tego, jak wygląda szukana ścieżka, nadal jest prawdziwe. Czyli albo ścieżka całkowicie zawiera się w którymś z poddrzew, albo kończy się w aktualnym korzeniu, albo przez niego przechodzi. Pierwszy przypadek załatwia rekursja, drugi i trzeci też daje się rozwiązać. Czyli cała idea jest taka, że chcielibyśmy przerobić algorytm działający w
. Dlaczego? Każda ścieżka odpowiada w nim ciągowi coraz mniejszych spójnych składowych, z których każde dwie kolejne zawierają się w sobie, a co więcej rozmiar mniejszej nie przekracza połowy rozmiaru większej. Zauważmy też, że całe rozumowanie dotyczące tego, jak wygląda szukana ścieżka, nadal jest prawdziwe. Czyli albo ścieżka całkowicie zawiera się w którymś z poddrzew, albo kończy się w aktualnym korzeniu, albo przez niego przechodzi. Pierwszy przypadek załatwia rekursja, drugi i trzeci też daje się rozwiązać. Czyli cała idea jest taka, że chcielibyśmy przerobić algorytm działający w 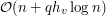 tak, aby operował na drzewie
tak, aby operował na drzewie 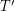 . Tak naprawdę jedynym problemem, jaki musimy rozwiązać, jest to, że nie potrafimy wyliczać idąc do góry w
. Tak naprawdę jedynym problemem, jaki musimy rozwiązać, jest to, że nie potrafimy wyliczać idąc do góry w 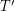 najdłuższej ścieżki prowadzącej do wierzchołka z jakiegoś jego poddrzewa. Skoro tego nie umiemy, to na początku działania algorytmu spamiętujemy taką informację. A dokładniej, dla każdego wierzchołka
najdłuższej ścieżki prowadzącej do wierzchołka z jakiegoś jego poddrzewa. Skoro tego nie umiemy, to na początku działania algorytmu spamiętujemy taką informację. A dokładniej, dla każdego wierzchołka  pamiętamy jego odległości do wszystkich jego przodków w
pamiętamy jego odległości do wszystkich jego przodków w 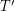 . Mając taką informację możemy postępować podobnie jak w poprzednim rozwiązaniu, otrzymując algorytm działający w czasie
. Mając taką informację możemy postępować podobnie jak w poprzednim rozwiązaniu, otrzymując algorytm działający w czasie 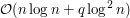 i zużywający
i zużywający 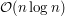 pamięci.
pamięci.
Podsumowanie
Cały algorytm wygląda w następujący sposób: na początku konstruujemy drzewo 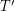 . To nie jest specjalnie skomplikowane, postępujemy zgodnie ze schematem z dowodu istnienia Fajnych Wierzchołków. Ta część wymaga tylko czasu
. To nie jest specjalnie skomplikowane, postępujemy zgodnie ze schematem z dowodu istnienia Fajnych Wierzchołków. Ta część wymaga tylko czasu 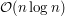 . Dlaczego nie
. Dlaczego nie 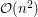 ? Każdy wierzchołek bierze udział w co najwyżej
? Każdy wierzchołek bierze udział w co najwyżej 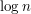 procedurach obliczania Fajnego Wierzchołka. Następnie spamiętujemy odpowiednie odległości, ten krok można łatwo połączyć z poprzedni. Mając te struktury, operacje
procedurach obliczania Fajnego Wierzchołka. Następnie spamiętujemy odpowiednie odległości, ten krok można łatwo połączyć z poprzedni. Mając te struktury, operacje  i
i  są już bardzo łatwe. W najprostszej wersji dla każdego wierzchołka
są już bardzo łatwe. W najprostszej wersji dla każdego wierzchołka 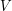 potrzebujemy trzymać:
potrzebujemy trzymać:
- dla jego każdego syna
 kopiec ze ścieżkami z
kopiec ze ścieżkami z  do białych wierzchołków zawartych w poddrzewie
do białych wierzchołków zawartych w poddrzewie  ,
,
- nadrzędny kopiec przechowujący maksima z kopców dla poszczególnych synów,
- zmienną przechowującą aktualną odpowiedź dla poddrzewa
 .
.
Powodzenia w kodowaniu!



 ma oczywiście rozmiar mniejszy niż
ma oczywiście rozmiar mniejszy niż 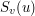 . Stąd rozmiar największej spójnej składowej cały czas się zmniejsza, zatem nasz proces musi się prędzej lub później skończyć.
. Stąd rozmiar największej spójnej składowej cały czas się zmniejsza, zatem nasz proces musi się prędzej lub później skończyć.


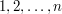 . Każda z jego
. Każda z jego 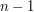 krawędzi ma przyporządkowaną całkowitoliczbową wagę (być może ujemną). Dodatkowo każdy wierzchołek jest pomalowany na czarno lub biało. Na samym początku wszystkie wierzchołki są białe. Niech
krawędzi ma przyporządkowaną całkowitoliczbową wagę (być może ujemną). Dodatkowo każdy wierzchołek jest pomalowany na czarno lub biało. Na samym początku wszystkie wierzchołki są białe. Niech 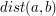 oznacza wagę (jedynej) ścieżki między wierzchołkiem
oznacza wagę (jedynej) ścieżki między wierzchołkiem  i
i  . Naszym celem jest (wydajne!) przetworzenie ciągu
. Naszym celem jest (wydajne!) przetworzenie ciągu 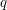 operacji, z których każda to
operacji, z których każda to
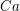 , zmień kolor wierzchołka
, zmień kolor wierzchołka  , oblicz wagę najcięższej ścieżki między (dowolnymi) dwoma białymi wierzchołkami.
, oblicz wagę najcięższej ścieżki między (dowolnymi) dwoma białymi wierzchołkami.
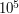 , wagi krawędzi należą do zakresu
, wagi krawędzi należą do zakresu ![$ [-1000 .. 1000] $](/files/tex/a7415aee109b1b01269b33e3f62897a7d097e407.png) .
.
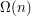 : trzeba popatrzeć przynajmniej raz na każdy wierzchołek. A czy istnieje algorytm, który działa dokładnie w takim czasie? Tak! Z pomocą przychodzi nam tutaj programowanie dynamiczne (czy też, dla tych z Was, którzy czują się bardziej matematykami, rozumowanie indukcyjne). Bazą indukcji jest drzewo składające się z jednego wierzchołka, dla którego bez problemu możemy obliczyć odpowiedź. W kroku indukcyjnym mamy całe, być może bardzo duże, drzewo. Wybierzmy jeden z wierzchołków
: trzeba popatrzeć przynajmniej raz na każdy wierzchołek. A czy istnieje algorytm, który działa dokładnie w takim czasie? Tak! Z pomocą przychodzi nam tutaj programowanie dynamiczne (czy też, dla tych z Was, którzy czują się bardziej matematykami, rozumowanie indukcyjne). Bazą indukcji jest drzewo składające się z jednego wierzchołka, dla którego bez problemu możemy obliczyć odpowiedź. W kroku indukcyjnym mamy całe, być może bardzo duże, drzewo. Wybierzmy jeden z wierzchołków  i ukorzeńmy w nim drzewo. Powiedzmy, że
i ukorzeńmy w nim drzewo. Powiedzmy, że 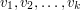 (
(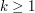 ). Możliwe są trzy sytuacje:
). Możliwe są trzy sytuacje:
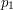 zawartą w podrzewie
zawartą w podrzewie 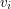 i
i 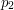 znajdującą się w poddrzewie
znajdującą się w poddrzewie 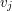 (
(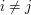 ). Każda z tych dwóch części jest najcięższą ścieżką zaczynającą się w białym wierzchołku i kończącą się w
). Każda z tych dwóch części jest najcięższą ścieżką zaczynającą się w białym wierzchołku i kończącą się w 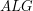 .
.
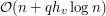 , gdzie
, gdzie 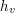 to wysokość drzewa zakorzenionego w (dowolnie wybranym) wierzchołku
to wysokość drzewa zakorzenionego w (dowolnie wybranym) wierzchołku 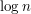 ? Uaktualniając wartości na ścieżce musimy wyznaczać nowe maksima (to jest najcięższe ścieżki zaczynająca się w białym wierzchołku i kończące się w korzeniu danego poddrzewo i najcięższa ścieżka w całym poddrzewie). Możemy albo za każdym razem przeglądać wszystkich synów danego wierzchołka na ścieżce (co nie jest najlepszym pomysłem), albo pamiętać te wartości w kolejce priorytetowej lub multisecie.
? Uaktualniając wartości na ścieżce musimy wyznaczać nowe maksima (to jest najcięższe ścieżki zaczynająca się w białym wierzchołku i kończące się w korzeniu danego poddrzewo i najcięższa ścieżka w całym poddrzewie). Możemy albo za każdym razem przeglądać wszystkich synów danego wierzchołka na ścieżce (co nie jest najlepszym pomysłem), albo pamiętać te wartości w kolejce priorytetowej lub multisecie.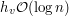 . Czasami jest to łatwe (na przykład w pełnym drzewie binarnym), a czasami niemożliwe... Zatem trafiliśmy w ślepą uliczkę? Nic bardziej mylnego!
. Czasami jest to łatwe (na przykład w pełnym drzewie binarnym), a czasami niemożliwe... Zatem trafiliśmy w ślepą uliczkę? Nic bardziej mylnego! będzie dowolnym drzewem o
będzie dowolnym drzewem o  wierzchołkach. Istnieje taki wierzchołek
wierzchołkach. Istnieje taki wierzchołek 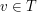 , że każda spójna składowa w
, że każda spójna składowa w 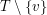 ma rozmiar nie większy niż
ma rozmiar nie większy niż 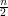 .
Jak się o tym przekonać? Niech
.
Jak się o tym przekonać? Niech 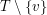 do spójnej składowej o rozmiarze przekraczającym
do spójnej składowej o rozmiarze przekraczającym  i powtarzamy całe rozumowanie. Czy takie postępowanie musi się kiedyś skończyć? Czy też może się zdarzyć, że wpadniemy w cykl? Niech
i powtarzamy całe rozumowanie. Czy takie postępowanie musi się kiedyś skończyć? Czy też może się zdarzyć, że wpadniemy w cykl? Niech 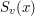 oznacza rozmiar składowej wierzchołka
oznacza rozmiar składowej wierzchołka  w
w 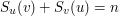
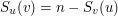
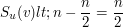
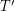 .
.
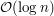 . Dlaczego? Każda ścieżka odpowiada w nim ciągowi coraz mniejszych spójnych składowych, z których każde dwie kolejne zawierają się w sobie, a co więcej rozmiar mniejszej nie przekracza połowy rozmiaru większej. Zauważmy też, że całe rozumowanie dotyczące tego, jak wygląda szukana ścieżka, nadal jest prawdziwe. Czyli albo ścieżka całkowicie zawiera się w którymś z poddrzew, albo kończy się w aktualnym korzeniu, albo przez niego przechodzi. Pierwszy przypadek załatwia rekursja, drugi i trzeci też daje się rozwiązać. Czyli cała idea jest taka, że chcielibyśmy przerobić algorytm działający w
. Dlaczego? Każda ścieżka odpowiada w nim ciągowi coraz mniejszych spójnych składowych, z których każde dwie kolejne zawierają się w sobie, a co więcej rozmiar mniejszej nie przekracza połowy rozmiaru większej. Zauważmy też, że całe rozumowanie dotyczące tego, jak wygląda szukana ścieżka, nadal jest prawdziwe. Czyli albo ścieżka całkowicie zawiera się w którymś z poddrzew, albo kończy się w aktualnym korzeniu, albo przez niego przechodzi. Pierwszy przypadek załatwia rekursja, drugi i trzeci też daje się rozwiązać. Czyli cała idea jest taka, że chcielibyśmy przerobić algorytm działający w 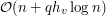 tak, aby operował na drzewie
tak, aby operował na drzewie 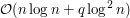 i zużywający
i zużywający 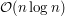 pamięci.
pamięci.
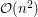 ? Każdy wierzchołek bierze udział w co najwyżej
? Każdy wierzchołek bierze udział w co najwyżej  są już bardzo łatwe. W najprostszej wersji dla każdego wierzchołka
są już bardzo łatwe. W najprostszej wersji dla każdego wierzchołka 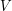 potrzebujemy trzymać:
potrzebujemy trzymać:


