Moim bodaj ulubionym zadaniem konkursowym jest zadanie za 500 z czwartej, czyli ostatniej zdalnej, rundy konkursu TopCoder Open 2006. Pewnie dlatego, że wskutek kilku ciekawych zbiegów okoliczności to zadanie okazało się mieć niespodziewany wpływ na historię moich startów w konkursach programistycznych, ale i nie tylko. Zacznijmy jednak od początku.
Przebieg rundy
Nadchodzi ostatnia runda eliminacji zdalnych w konkursie TopCoder Open 2006, jeszcze tylko ta runda i lecimy do Las Vegas. I wszystko byłoby dobrze (nawet stosunkowo dużo zawodników awansuje, bo 48), gdyby nie to, że runda jest o trzeciej w nocy czasu polskiego. Profesor Diks mawia, że wielcy mistrzowie wygrywają w każdych warunkach. Ja niestety bynajmniej się do tej grupy nie zaliczam, gdyż w środku nocy myślenie to zdecydowanie ostatnia rzecz, na jaką mam ochotę. Ponieważ była to już trzecia runda z rzędu o tak koszmarnej porze, wszyscy polscy uczestnicy intensywnie mobilizowali się do startu.
Runda rozpoczęła się bez większych niespodzianek, ot nieprzyjemne, koderskie zadanie za 250. Schody zaczęły się dalej. Otwieram zadanie za 500, ma przyjemnie krótką treść, którą można sparafrazować tak:
Dany jest ciąg liczb zerojedynkowych 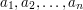
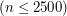 . Należy znaleźć niemalejący ciąg rzeczywisty
. Należy znaleźć niemalejący ciąg rzeczywisty 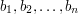 , dla którego wyrażenie:
, dla którego wyrażenie:
przyjmuje najmniejszą wartość, i zwrócić 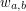 .
.
Pewne proste spostrzeżenia nasuwają się same. Dla ciągu a postaci: ileś zer, ileś jedynek, szukanym ciągiem  jest oczywiście ten sam ciąg. Z kolei dla ciągu postaci:
jest oczywiście ten sam ciąg. Z kolei dla ciągu postaci:  jedynek, a po nich
jedynek, a po nich  zer, ciąg
zer, ciąg  musi być stały. Faktycznie, zwiększając wartości pierwszych
musi być stały. Faktycznie, zwiększając wartości pierwszych  elementów ciągu
elementów ciągu  i zmniejszając pozostałe (oczywiście w granicach
i zmniejszając pozostałe (oczywiście w granicach ![$ [0,1] $](/files/tex/32d80deee5cba3c656aff775830cd425d6ceb118.png) ) na pewno zmniejszamy wartość
) na pewno zmniejszamy wartość 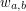 , a poprawiając w ten sposób, na pewno w końcu sprowadzimy dowolny ciąg
, a poprawiając w ten sposób, na pewno w końcu sprowadzimy dowolny ciąg  do stałego. Wartość jego elementów
do stałego. Wartość jego elementów  powinna minimalizować wartość wyrażenia:
powinna minimalizować wartość wyrażenia:
Korzystając z faktu, że powyższy wielomian kwadratowy przyjmuje minimum w miejscu zerowania się jego pochodnej:
otrzymujemy, że prawidłową wartością  jest
jest 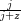 , czyli średnia arytmetyczna ze wszystkich wyrazów ciągu
, czyli średnia arytmetyczna ze wszystkich wyrazów ciągu  . I co dalej?
. I co dalej?
Niestety w tym miejscu pomysły na spostrzeżenia mi się zupełnie skończyły: nie bardzo widać, jak poradzić sobie z dowolnym ciągiem  . Rzut oka na ranking zawodów podpowiada, że nie tylko ja mam ten problem: dosłownie kilku zawodników poradziło sobie z zadaniem całkiem szybko (najszybszemu zajęło ok. 12 minut), reszcie nie idzie jednak tak gładko: równomiernie przez większość konkursu co minutę-dwie komuś udaje się wysłać rozwiązanie (dodam, że średni czas poprawnego zgłoszenia wyniósł w tym zadaniu coś ponad 36 minut) - ewidentnie zadanie wymaga jakiegoś sprytnego pomysłu. Otwarte w akcie desperacji zadanie za 1000 nie wygląda na takie, które miałbym jeszcze szansę zdążyć rozwiązać, stosunkowo powolnie pisane rozwiązanie zadania za 250 najpewniej nie da awansu, a tu już godzina zawodów mija (dla niewtajemniczonych: runda trwa 75 minut) i pomysłów na 500-tkę brak - a wspominałem już, że jest środek nocy?
. Rzut oka na ranking zawodów podpowiada, że nie tylko ja mam ten problem: dosłownie kilku zawodników poradziło sobie z zadaniem całkiem szybko (najszybszemu zajęło ok. 12 minut), reszcie nie idzie jednak tak gładko: równomiernie przez większość konkursu co minutę-dwie komuś udaje się wysłać rozwiązanie (dodam, że średni czas poprawnego zgłoszenia wyniósł w tym zadaniu coś ponad 36 minut) - ewidentnie zadanie wymaga jakiegoś sprytnego pomysłu. Otwarte w akcie desperacji zadanie za 1000 nie wygląda na takie, które miałbym jeszcze szansę zdążyć rozwiązać, stosunkowo powolnie pisane rozwiązanie zadania za 250 najpewniej nie da awansu, a tu już godzina zawodów mija (dla niewtajemniczonych: runda trwa 75 minut) i pomysłów na 500-tkę brak - a wspominałem już, że jest środek nocy?
W takim momencie można już tylko próbować zgadywać. Jedynym dobrym pomysłem po drodze wydaje się ten ze średnią arytmetyczną. Zacznijmy więc poszukiwanie  od samego ciągu
od samego ciągu  . Jeżeli jest on niemalejący, to możemy skończyć. Jeżeli nie, to wybierzmy jakiś fragment złożony z kolejnych jedynek, po którym następuje ciąg zer, i zastąpmy te dwa fragmenty jednym, którego wyraz to średnia arytmetyczna wszystkich tych zer i jedynek. I teraz możemy to postępowanie powtarzać w kółko: jeżeli sąsiadują ze sobą dwa stałe fragmenty ciągu, z których pierwszy ma wyraz większy od drugiego, to zastępujemy oba fragmenty jednym, którego wyraz jest średnią arytmetyczną wszystkich zastępowanych wyrazów. Nie jest jasne, czy za pomocą takich operacji zawsze uzyska się optymalny ciąg
. Jeżeli jest on niemalejący, to możemy skończyć. Jeżeli nie, to wybierzmy jakiś fragment złożony z kolejnych jedynek, po którym następuje ciąg zer, i zastąpmy te dwa fragmenty jednym, którego wyraz to średnia arytmetyczna wszystkich tych zer i jedynek. I teraz możemy to postępowanie powtarzać w kółko: jeżeli sąsiadują ze sobą dwa stałe fragmenty ciągu, z których pierwszy ma wyraz większy od drugiego, to zastępujemy oba fragmenty jednym, którego wyraz jest średnią arytmetyczną wszystkich zastępowanych wyrazów. Nie jest jasne, czy za pomocą takich operacji zawsze uzyska się optymalny ciąg  , ale nie ma już czasu na dowodzenie. Kilka minut szybkiego kodowania i rozwiązanie gotowe. Sprawdzam na solidnie wyglądających testach przykładowych - działa. Wysyłam kilka minut przed końcem, po czym w oczekiwaniu na wyniki spędzam jedne z bardziej nerwowych 30 minut życia.
, ale nie ma już czasu na dowodzenie. Kilka minut szybkiego kodowania i rozwiązanie gotowe. Sprawdzam na solidnie wyglądających testach przykładowych - działa. Wysyłam kilka minut przed końcem, po czym w oczekiwaniu na wyniki spędzam jedne z bardziej nerwowych 30 minut życia.
Czemu to działa?
Na moje szczęście okazało się, że opisane rozwiązanie było poprawne i dzięki temu, podobnie jak rekordowo dużej liczbie Polaków, udało mi się awansować po raz pierwszy w życiu do półfinału konkursu TCO. Żeby jednak nie zakończyć tego opisu samym zgadywaniem, przedstawię w skrócie uzasadnienie poprawności powyższego rozwiązania.
Wprowadźmy podstawową terminologię. Dla danego ciągu  , szukany niemalejący ciąg
, szukany niemalejący ciąg  nazwiemy najlepszą aproksymacją (tj. najlepszym przybliżeniem), natomiast wartość
nazwiemy najlepszą aproksymacją (tj. najlepszym przybliżeniem), natomiast wartość 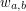 nazwiemy błędem aproksymacji. Zacznijmy od pseudokodu opisanego wyżej rozwiązania. Korzystamy w nim z listy L, reprezentującej aktualną postać przekształcanego ciągu (zaczynamy od listy reprezentującej ciąg
nazwiemy błędem aproksymacji. Zacznijmy od pseudokodu opisanego wyżej rozwiązania. Korzystamy w nim z listy L, reprezentującej aktualną postać przekształcanego ciągu (zaczynamy od listy reprezentującej ciąg  ). Lista L zawiera pary postaci: (x - element będący najlepszą aproksymacją fragmentu ciągu
). Lista L zawiera pary postaci: (x - element będący najlepszą aproksymacją fragmentu ciągu  , ilość - liczba elementów ciągu w tym fragmencie). Ponieważ jest to tylko pseudokod, możemy sobie w nim pozwolić na pewne nadużycie: zakładamy, że kolejne elementy listy możemy indeksować liczbami od 1 do L.size(), zupełnie jak w przypadku tablicy (korzystamy przy tym zawsze tylko z kolejnych indeksów).
, ilość - liczba elementów ciągu w tym fragmencie). Ponieważ jest to tylko pseudokod, możemy sobie w nim pozwolić na pewne nadużycie: zakładamy, że kolejne elementy listy możemy indeksować liczbami od 1 do L.size(), zupełnie jak w przypadku tablicy (korzystamy przy tym zawsze tylko z kolejnych indeksów).
1
2
3
4
5
6
7
8
9
10
11
12
| for i = 1 to n do
L.insert(a(i), 1);
i = 1;
while (i < L.size()) {
if (L[i].x > L[i + 1].x) {
L[i].x = średnia(L[i].x, L[i].ilość, L[i + 1].x, L[i + 1].ilość);
L[i].ilość += L[i + 1].ilość;
L.erase(L[i + 1]);
if (i > 1) --i;
} else ++i;
}
return L; |
Jeżeli warunek L[i].x > L[i + 1].x zachodzi, to zgodnie z wcześniejszym nieformalnym opisem dokonujemy wówczas scalenia kolejnych fragmentów ciągu, przydzielając wynikowemu fragmentowi wartość będącą średnią arytmetyczną z wszystkich jego wyrazów. Odpowiada za to funkcja średnia, która zwraca wynik zgodnie ze wzorem:
Uzasadnienie poprawności tego wzoru jest natychmiastowe, jeżeli zauważyć, że pole x reprezentuje średnią z elementów ciągu w  -tym fragmencie, a zatem wyrażenie postaci L[i].x * L[i].ilość oznacza sumę elementów
-tym fragmencie, a zatem wyrażenie postaci L[i].x * L[i].ilość oznacza sumę elementów  -tego fragmentu ciągu. Co więcej, łatwo zauważyć, że w wynikowej liście L wartości L[i].x są posortowane niemalejąco (dbamy o to m.in. w linii "if (i > 1) --i;"), czyli reprezentują poprawną niemalejącą aproksymację ciągu
-tego fragmentu ciągu. Co więcej, łatwo zauważyć, że w wynikowej liście L wartości L[i].x są posortowane niemalejąco (dbamy o to m.in. w linii "if (i > 1) --i;"), czyli reprezentują poprawną niemalejącą aproksymację ciągu  .
.
Złożoność czasowa powyższego rozwiązania to 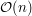 . Aby to uzasadnić, wystarczy przyjrzeć się parametrowi
. Aby to uzasadnić, wystarczy przyjrzeć się parametrowi 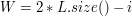 . Przed pierwszym obrotem pętli while
. Przed pierwszym obrotem pętli while 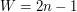 , a przy każdym obrocie pętli parametr ten zmniejsza się co najmniej o jeden i pozostaje cały czas dodatni. Widać więc, że ograniczenie
, a przy każdym obrocie pętli parametr ten zmniejsza się co najmniej o jeden i pozostaje cały czas dodatni. Widać więc, że ograniczenie 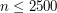 z konkursu jest tak naprawdę bardzo łagodne.
z konkursu jest tak naprawdę bardzo łagodne.
Wiemy już, że nasz algorytm jest bardzo efektywny oraz że zwraca w wyniku ciąg niemalejący. Pozostaje najtrudniejsza kwestia: uzasadnić, że jest on najlepszą aproksymacją ciągu  . W tym celu trzeba pokazać trzy rzeczy (z pierwszych dwóch wynika, że wynikowy ciąg w algorytmie jest kawałkami najlepszą aproksymacją ciągu
. W tym celu trzeba pokazać trzy rzeczy (z pierwszych dwóch wynika, że wynikowy ciąg w algorytmie jest kawałkami najlepszą aproksymacją ciągu  , natomiast z trzeciego, że wówczas jest już najlepszą aproksymacją całego ciągu):
, natomiast z trzeciego, że wówczas jest już najlepszą aproksymacją całego ciągu):
- Jeżeli najlepsza aproksymacja jednego fragmentu ciągu
 jest ciągiem stałym o elementach równych
jest ciągiem stałym o elementach równych  , a najlepsza aproksymacja drugiego - ciągiem stałym o elementach równych
, a najlepsza aproksymacja drugiego - ciągiem stałym o elementach równych  oraz
oraz 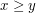 , to najlepsza aproksymacja ciągu będącego sklejeniem tych dwóch fragmentów jest także ciągiem stałym.
, to najlepsza aproksymacja ciągu będącego sklejeniem tych dwóch fragmentów jest także ciągiem stałym.
- Jeżeli najlepsza aproksymacja fragmentu ciągu
 jest ciągiem stałym, to jego wyrazem jest średnia arytmetyczna z wyrazów tego fragmentu.
jest ciągiem stałym, to jego wyrazem jest średnia arytmetyczna z wyrazów tego fragmentu.
- Jeżeli jakiś ciąg
 stanowi najlepszą aproksymację każdego z fragmentów ciągu
stanowi najlepszą aproksymację każdego z fragmentów ciągu  (liczba tych fragmentów może być dowolna, ważne aby pokrywały cały ciąg
(liczba tych fragmentów może być dowolna, ważne aby pokrywały cały ciąg  ), to jest on najlepszą aproksymacją całego ciągu
), to jest on najlepszą aproksymacją całego ciągu  .
.
Drugi z powyższych faktów można uzasadnić, podobnie jak w szczególnym, zero-jedynkowym przypadku, za pomocą argumentu z pochodną wyrażenia 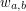 . Uzasadnienie trzeciego faktu polega na rozbiciu wzoru na
. Uzasadnienie trzeciego faktu polega na rozbiciu wzoru na 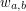 na kawałki odpowiadające wspomnianym fragmentom ciągu
na kawałki odpowiadające wspomnianym fragmentom ciągu  . Niestety, dokładny dowód pierwszego faktu jest bardziej skomplikowany i dosyć techniczny. W (telegraficznym) skrócie polega on na tym, że startujemy od jakiejkolwiek najlepszej niemalejącej aproksymacji
. Niestety, dokładny dowód pierwszego faktu jest bardziej skomplikowany i dosyć techniczny. W (telegraficznym) skrócie polega on na tym, że startujemy od jakiejkolwiek najlepszej niemalejącej aproksymacji  sklejenia dwóch fragmentów i pokazujemy, jak w kolejnych krokach modyfikować ciąg
sklejenia dwóch fragmentów i pokazujemy, jak w kolejnych krokach modyfikować ciąg  tak, aby stał się najpierw stały na każdym ze sklejanych fragmentów, a następnie w ogóle stały. Każde z opisanych przekształceń polega na ciągłym podciąganiu lub opuszczaniu pewnych fragmentów ciągu
tak, aby stał się najpierw stały na każdym ze sklejanych fragmentów, a następnie w ogóle stały. Każde z opisanych przekształceń polega na ciągłym podciąganiu lub opuszczaniu pewnych fragmentów ciągu  , a wykorzystujemy przy tym fakt, że funkcja określająca błąd aproksymacji ciągu ciągiem stałym jest kwadratowa i wypukła.
, a wykorzystujemy przy tym fakt, że funkcja określająca błąd aproksymacji ciągu ciągiem stałym jest kwadratowa i wypukła.
Podane uzasadnienie poprawności algorytmu jest bardzo niepełne. Pod koniec artykułu można znaleźć odnośnik do pełnego dowodu poprawności.
Dalsza historia zadania
Jednym z zadań na Bałtyckiej Olimpiadzie Informatycznej BOI 2004 było zadanie Sequence. Okazało się ono bardzo trudne i zostało rozwiązane poprawnie tylko przez zwycięzcę tych zawodów - Filipa Wolskiego. Zadanie to polegało także na znalezieniu niemalejącego (w oryginale: rosnącego i całkowitoliczbowego, ale nie miało to aż takiego znaczenia) ciągu  , który najlepiej aproksymuje zadany ciąg
, który najlepiej aproksymuje zadany ciąg  , tyle że miarą błędu aproksymacji było:
, tyle że miarą błędu aproksymacji było:
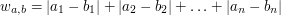 | |
Oryginalne, bardzo pomysłowe rozwiązanie Filipa (złożoność czasowa 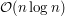 ) jest opisane w Delcie 11/2007. Co ciekawe jednak, rozwiązanie zadania z TopCodera daje się wykorzystać także i w tym zadaniu! Wystarczy w nim podmienić funkcję średnia z powyższego pseudokodu funkcją, która wyznacza najlepszą stałą aproksymację ciągu zgodnie z nową postacią wzoru na wa,b, a jest nią mianowicie mediana ciągu. (Uzasadnienie poprawności tego stwierdzenia oraz sprawdzenie, że wszystkie opisane w poprzedniej sekcji fakty działają także i w tym przypadku, pomijam). Pozostaje jeszcze pytanie, jak efektywnie takie mediany wyznaczać.
) jest opisane w Delcie 11/2007. Co ciekawe jednak, rozwiązanie zadania z TopCodera daje się wykorzystać także i w tym zadaniu! Wystarczy w nim podmienić funkcję średnia z powyższego pseudokodu funkcją, która wyznacza najlepszą stałą aproksymację ciągu zgodnie z nową postacią wzoru na wa,b, a jest nią mianowicie mediana ciągu. (Uzasadnienie poprawności tego stwierdzenia oraz sprawdzenie, że wszystkie opisane w poprzedniej sekcji fakty działają także i w tym przypadku, pomijam). Pozostaje jeszcze pytanie, jak efektywnie takie mediany wyznaczać.
Otóż z każdym elementem listy L wystarczy związać jakieś drzewo zrównoważone 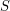 (np. AVL czy czerwono-czarne) do przechowywania wszystkich elementów ciągu odpowiadających temu elementowi listy. Korzystając z takiego drzewa, można w czasie
(np. AVL czy czerwono-czarne) do przechowywania wszystkich elementów ciągu odpowiadających temu elementowi listy. Korzystając z takiego drzewa, można w czasie 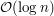 wyznaczyć medianę z elementów w nim zawartych. Pozostaje jedynie problem, jak aktualizować takie drzewa w momencie scalania elementów listy, czyli po prostu jak scalać takie drzewa. Okazuje się, że wystarczy przenieść wszystkie elementy z mniejszego drzewa do większego, tzn. kolejno usuwać z mniejszego i wstawiać do większego. Wówczas co prawda pojedyncze scalenie może zająć dużo czasu, ale łączny koszt wszystkich scaleń będzie
wyznaczyć medianę z elementów w nim zawartych. Pozostaje jedynie problem, jak aktualizować takie drzewa w momencie scalania elementów listy, czyli po prostu jak scalać takie drzewa. Okazuje się, że wystarczy przenieść wszystkie elementy z mniejszego drzewa do większego, tzn. kolejno usuwać z mniejszego i wstawiać do większego. Wówczas co prawda pojedyncze scalenie może zająć dużo czasu, ale łączny koszt wszystkich scaleń będzie 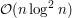 . Jest tak dlatego, że każdy element
. Jest tak dlatego, że każdy element 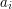 zostanie przeniesiony w całym algorytmie co najwyżej
zostanie przeniesiony w całym algorytmie co najwyżej 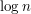 razy, gdyż podczas takiego przenoszenia rozmiar drzewa, do którego należy (w sensie: liczba elementów ciągu znajdujących się w drzewie), wzrasta co najmniej dwukrotnie. Ponieważ koszt czasowy pojedynczego przeniesienia to
razy, gdyż podczas takiego przenoszenia rozmiar drzewa, do którego należy (w sensie: liczba elementów ciągu znajdujących się w drzewie), wzrasta co najmniej dwukrotnie. Ponieważ koszt czasowy pojedynczego przeniesienia to 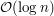 , a łącznie elementów mamy
, a łącznie elementów mamy  , więc faktycznie złożoność czasowa algorytmu to
, więc faktycznie złożoność czasowa algorytmu to 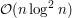 .
.
Idąc dalej, można rozwiązać zadanie podobne do dwóch już przedstawionych, w którym minimalizujemy wartość wyrażenia:
W tym celu można także zastosować ogólny schemat, w którym tym razem zamiast operacji średnia należy wstawić średnią z minimalnego i maksymalnego elementu fragmentu ciągu. (Sprawdzenie, że tak właśnie wygląda najlepsza stała aproksymacja w tym przypadku, jest natychmiastowe). Otrzymujemy wówczas rozwiązanie o złożoności czasowej 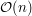 . Istnieje także znacznie prostsze koncepcyjnie rozwiązanie tej wersji zadania o tej samej złożoności, którego jednak w tym miejscu nie przytoczę. Wszystkie trzy opisane zadania można rozwiązać w Staszicowym serwisie KI: Aproksymacja, Aproksymacja kontratakuje i Powrót aproksymacji.
. Istnieje także znacznie prostsze koncepcyjnie rozwiązanie tej wersji zadania o tej samej złożoności, którego jednak w tym miejscu nie przytoczę. Wszystkie trzy opisane zadania można rozwiązać w Staszicowym serwisie KI: Aproksymacja, Aproksymacja kontratakuje i Powrót aproksymacji.
Ale to nie koniec. Otóż okazuje się, że wszystkie trzy występujące w powyższych zadaniach wzory na 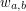 są szczególnymi przypadkami czegoś, co w matematyce określa się mianem
są szczególnymi przypadkami czegoś, co w matematyce określa się mianem  -tej normy
-tej normy  -wymiarowego wektora
-wymiarowego wektora 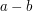 . Wyraża się ona wzorem:
. Wyraża się ona wzorem:
dla  całkowitego dodatniego oraz:
całkowitego dodatniego oraz:
dla 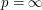 . Jak można się domyślić, odpowiednio zmodyfikowane rozwiązanie zadania z TopCodera działa także i w tym ogólnym przypadku. Pozwala to wypracować ogólny algorytm działający dla wszystkich
. Jak można się domyślić, odpowiednio zmodyfikowane rozwiązanie zadania z TopCodera działa także i w tym ogólnym przypadku. Pozwala to wypracować ogólny algorytm działający dla wszystkich  -tych norm, ale także i efektywne algorytmy dla innych wartości parametru
-tych norm, ale także i efektywne algorytmy dla innych wartości parametru  , chociażby dla
, chociażby dla 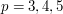 . Dzięki poczynionym uogólnieniom, nocne rozwiązywanie pewnego zadania z konkursu doprowadziło mnie nie tylko do Las Vegas, ale także do napisania pracy licencjackiej z matematyki na temat aproksymacji ciągów ciągami monotonicznymi. I to wreszcie przesądziło o fakcie, że wyjściowe zadanie plasuje się na pierwszym miejscu wśród moich ulubionych.
. Dzięki poczynionym uogólnieniom, nocne rozwiązywanie pewnego zadania z konkursu doprowadziło mnie nie tylko do Las Vegas, ale także do napisania pracy licencjackiej z matematyki na temat aproksymacji ciągów ciągami monotonicznymi. I to wreszcie przesądziło o fakcie, że wyjściowe zadanie plasuje się na pierwszym miejscu wśród moich ulubionych.





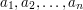
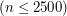 . Należy znaleźć niemalejący ciąg rzeczywisty
. Należy znaleźć niemalejący ciąg rzeczywisty 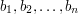 , dla którego wyrażenie:
, dla którego wyrażenie: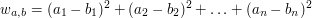
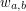 .
. jest oczywiście ten sam ciąg. Z kolei dla ciągu postaci:
jest oczywiście ten sam ciąg. Z kolei dla ciągu postaci:  jedynek, a po nich
jedynek, a po nich  zer, ciąg
zer, ciąg ![$ [0,1] $](/files/tex/32d80deee5cba3c656aff775830cd425d6ceb118.png) ) na pewno zmniejszamy wartość
) na pewno zmniejszamy wartość  powinna minimalizować wartość wyrażenia:
powinna minimalizować wartość wyrażenia: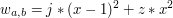
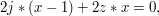
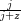 , czyli średnia arytmetyczna ze wszystkich wyrazów ciągu
, czyli średnia arytmetyczna ze wszystkich wyrazów ciągu  . I co dalej?
. I co dalej?![$$\frac{L[i].x * L[i].ilość + L[i + 1].x * L[i + 1].ilość}{L[i].ilość + L[i + 1].ilość}$$](/files/tex/ae75c27d2c4dbbeaffd745d39828a998958a1539.png)
 -tym fragmencie, a zatem wyrażenie postaci
-tym fragmencie, a zatem wyrażenie postaci 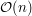 . Aby to uzasadnić, wystarczy przyjrzeć się parametrowi
. Aby to uzasadnić, wystarczy przyjrzeć się parametrowi 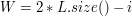 . Przed pierwszym obrotem pętli while
. Przed pierwszym obrotem pętli while 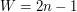 , a przy każdym obrocie pętli parametr ten zmniejsza się co najmniej o jeden i pozostaje cały czas dodatni. Widać więc, że ograniczenie
, a przy każdym obrocie pętli parametr ten zmniejsza się co najmniej o jeden i pozostaje cały czas dodatni. Widać więc, że ograniczenie 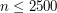 z konkursu jest tak naprawdę bardzo łagodne.
z konkursu jest tak naprawdę bardzo łagodne. oraz
oraz 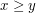 , to najlepsza aproksymacja ciągu będącego sklejeniem tych dwóch fragmentów jest także ciągiem stałym.
, to najlepsza aproksymacja ciągu będącego sklejeniem tych dwóch fragmentów jest także ciągiem stałym. sklejenia dwóch fragmentów i pokazujemy, jak w kolejnych krokach modyfikować ciąg
sklejenia dwóch fragmentów i pokazujemy, jak w kolejnych krokach modyfikować ciąg 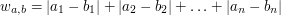
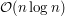 ) jest opisane w
) jest opisane w 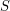 (np.
(np. 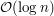 wyznaczyć medianę z elementów w nim zawartych. Pozostaje jedynie problem, jak aktualizować takie drzewa w momencie scalania elementów listy, czyli po prostu jak scalać takie drzewa. Okazuje się, że wystarczy przenieść wszystkie elementy z mniejszego drzewa do większego, tzn. kolejno usuwać z mniejszego i wstawiać do większego. Wówczas co prawda pojedyncze scalenie może zająć dużo czasu, ale łączny koszt wszystkich scaleń będzie
wyznaczyć medianę z elementów w nim zawartych. Pozostaje jedynie problem, jak aktualizować takie drzewa w momencie scalania elementów listy, czyli po prostu jak scalać takie drzewa. Okazuje się, że wystarczy przenieść wszystkie elementy z mniejszego drzewa do większego, tzn. kolejno usuwać z mniejszego i wstawiać do większego. Wówczas co prawda pojedyncze scalenie może zająć dużo czasu, ale łączny koszt wszystkich scaleń będzie 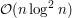 . Jest tak dlatego, że każdy element
. Jest tak dlatego, że każdy element 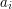 zostanie przeniesiony w całym algorytmie co najwyżej
zostanie przeniesiony w całym algorytmie co najwyżej 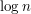 razy, gdyż podczas takiego przenoszenia rozmiar drzewa, do którego należy (w sensie: liczba elementów ciągu znajdujących się w drzewie), wzrasta co najmniej dwukrotnie. Ponieważ koszt czasowy pojedynczego przeniesienia to
razy, gdyż podczas takiego przenoszenia rozmiar drzewa, do którego należy (w sensie: liczba elementów ciągu znajdujących się w drzewie), wzrasta co najmniej dwukrotnie. Ponieważ koszt czasowy pojedynczego przeniesienia to  , więc faktycznie złożoność czasowa algorytmu to
, więc faktycznie złożoność czasowa algorytmu to 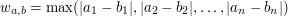
 -tej
-tej 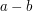 . Wyraża się ona wzorem:
. Wyraża się ona wzorem: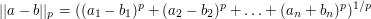
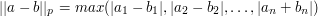
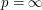 . Jak można się domyślić, odpowiednio zmodyfikowane rozwiązanie zadania z TopCodera działa także i w tym ogólnym przypadku. Pozwala to wypracować ogólny algorytm działający dla wszystkich
. Jak można się domyślić, odpowiednio zmodyfikowane rozwiązanie zadania z TopCodera działa także i w tym ogólnym przypadku. Pozwala to wypracować ogólny algorytm działający dla wszystkich 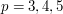 . Dzięki poczynionym uogólnieniom, nocne rozwiązywanie pewnego zadania z konkursu doprowadziło mnie nie tylko do Las Vegas, ale także do napisania
. Dzięki poczynionym uogólnieniom, nocne rozwiązywanie pewnego zadania z konkursu doprowadziło mnie nie tylko do Las Vegas, ale także do napisania 

