Football
03.06.2009 - Eryk Kopczyński
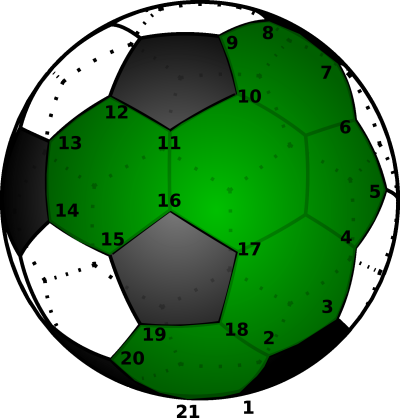
   W tym artykule przedstawiam jedno z ulubionych zadań mojego autorstwa. Zostało ono użyte na zawodach CEPC '03 (Central European Programming Contest) jako zadanie F (chociaż w trakcie pracy było nazywane raczej foo — skrót od Football). Dla pierwszej drużyny, która wysłała prawidłowe rozwiązanie, była ufundowana dodatkowa nagroda — piłka nożna. Podczas całych zawodów udało się to trzem drużynom: z Akademii Górniczo-Hutniczej, z Uniwersytetu Wrocławskiego, i z Uniwersytetu Warszawskiego. Najszybsza była drużyna z AGH i to ona wygrała piłkę, natomiast drużyna z UW wygrała cały konkurs (dzięki czemu awansowała do finałów). Treść zadaniaEryk ma klasyczną piłkę nożną złożoną z 32 kawałków skóry — 12 czarnych pięciokątów i 20 białych sześciokątów. Każdy pięciokąt styka się z 5 sześciokątami, a każdy sześciokąt styka się z 3 pięciokątami i 3 sześciokątami. Eryk narysował wielokąt (tzn. linię zamkniętą bez samoprzecięć) na krawędziach między kawałkami skóry. Wielokąt podzielił kulę na dwie części, Eryk pomalował jedną z nich na zielono.
Masz dany opis wielokąta. Czy umiesz policzyć liczbę białych, czarnych, i zielonych kawałków skóry na piłce? WejścieW pierwszej linii wejścia podana jest liczba n oznaczająca liczbę wierzchołków wielokąta. W drugiej podane jest n liczb całkowitych a1, a2, ..., an oddzielonych spacjami. Liczba ai (równa 1 lub 2) jest liczbą zielonych kawałków stykających się w i-tym wierzchołku wielokąta. Bok wielokąta łączący n-ty i pierwszy wierzchołek zawsze leży między dwoma sześciokątami. WyjścieNależy wypisać trzy liczby b, w i g. Są to odpowiednio liczby czarnych, białych, i zielonych kawałków. PrzykładDla wejścia: 21 prawidłową odpowiedzią jest: 11 15 6
Jak widzimy, w zadaniu przydaje się wyobraźnia przestrzenna. Może być przydatne narysowanie struktury piłki nożnej, ale jak to zrobić na kartce? Autor jednego z rozwiązań wzorcowych używał do tego pomarańczy. Pomarańcze były dostępne również podczas zawodów, także my (czyli sędziowie monitorujący przebieg zawodów i odpowiadający na pytania) zastanawialiśmy sie, czy któraś z drużyn również wpadnie na ten pomysł...
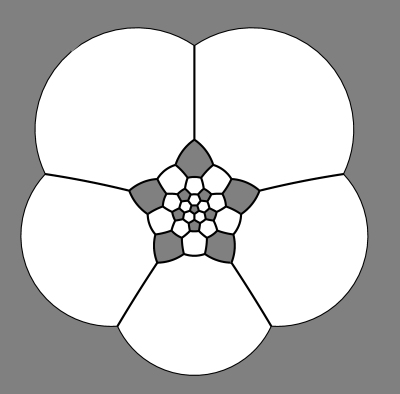
Rozrysowanie całego grafuRozwiązaniem bezpośrednim jest rozpisanie całej struktury piłki nożnej w jakiejś tablicy, rysowanie wielokąta na tej strukturze, i policzenie, które ściany (pięciokąty i sześciokąty) są wewnątrz wielokąta, które na zewnątrz. Chyba najprościej to zrobić w ten sposób, że wierzchołkami grafu są ściany, a krawędziami są krawędzie między nimi. Taki graf ma 32 wierzchołków i 90 krawędzi, także daje się go rozrysować w trakcie 5 godzin zawodów (być może przy pomocy pomarańczy), ale teraz nie będziemy tego robić. Rysowanie wielokąta polega na tym, że zaznaczamy krawędzie, po których przeszliśmy. Potem wystarczy policzyć wierzchołki każdego rodzaju w każdej z dwóch spójnych składowych grafu, który powstaje po eliminacji zaznaczonych krawędzi. Być może można sobie jakoś uprościć zadanie korzystając z wielu symetrii piłki nożnej (dzięki którym moglibyśmy wpisywać tylko część grafu, reszta byłaby symetryczna). Automatyczne budowanie grafuOpis piłki z zadania jest jednoznaczny — jeśli na piłce będziemy rysować pięciokąty i sześciokąty tak, żeby każdy pięciokąt stykał się z 5 sześciokątami, a każdy sześciokąt z 3 pięciokątami i 3 sześciokątami na przemian, to otrzymamy prawidłową strukturę piłki nożnej (z 12 pięciokątami i 20 sześciokątami). Łatwo to sprawdzić na płaszczyźnie — rysujemy najpierw pięciokąt, do każdego z jego boków dobudowujemy sześciokąt, tam, gdzie sześciokąty się stykają dobudowujemy nowe pięciokąty, itd. — otrzymamy wtedy oczywiście rzut stereograficzny piłki. Jeśli dobrze pamiętam, to rozwiązanie zwycięskiej drużyny z UW było oparte właśnie na tym spostrzeżeniu — samodzielnie budowało graf piłki nożnej zgodnie z podanymi zasadami. Dokładnych szczegółów nie będę podawał, gdyż kolejne rozwiązanie jest ciekawsze; zainteresowani mogą spróbować samemu zaimplementować taki pomysł. Liczenie pięciokątów i sześciokątów przy brzegu
Policzmy, ile kątów leżących przy brzegu wielokąta na jego zewnątrz jest czarnymi kątami pięciokątów, a ile jest białymi kątami sześciokątów. Przykładowo, dla wielokąta z przykładu mamy 18 czarnych kątów (położonych przy wierzchołkach numer 1, 2, 3, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21) i 16 białych kątów (1, 3, 4, 5 dwa razy, 6, 7, 8, 9, 12, 13, 14, 15, 19, 20, 21). Oznaczmy liczbę czarnych kątów przez eb, białych kątów przez ew. Okazuje się, że rozwiązanie
daje się policzyć, znając same liczby n, eb i ew (n to n z zadania, czyli liczba wierzchołków zielonego wielokąta). W dodatku liczby, o które prosi nas zadanie, zależą w sposób liniowy od tych trzech wartości.
int tab[3][2][4] = {A jak znaleźć liniową zależność między n, eb i ew? Można to zrobić na dwa sposoby. Wzór Eulera
Ten wzór chyba powinien być znany wszystkim lepszym zawodnikom: dla grafu płaskiego (albo narysowanego na sferze, jak w naszym zadaniu) liczba wierzchołków N, liczba ścian F i liczba krawędzi M spełniają równanie N+F = M+2. Na przykład, zanim pomalujemy piłkę nożną, było 32 ścian, 60 wierzchołków, i 90 krawędzi (32+60 = 90+2). Wzór Eulera albo związana z nim charakterystyka Eulera może nieoczekiwanie przydać się do trikowego rozwiązania jakiegoś problemu (zwykle liczenie ścian jest trudne, a wierzchołków i krawędzi bardzo łatwe; jeśli w zadaniu chodzi o liczenie ścian, to wzór Eulera łatwo daje nam rozwiązanie. Trzeba tylko uważać, żeby obszary z zadania były rzeczywiście ścianami, czyli nie dało ich się podzielić krawędzią tak, by obszar się nie rozpadł — jest to równoważne temu, że graf jest spójny). Innym ciekawym przykładem programu korzystającego z charakterystyki Eulera jest ten program, który należy kompilować z opcją -Dif=while. (Przykładowym wejściem do programu jest ten plik , a wyjaśnienie jest tutaj.)
Geometria sfery
Inspiracją do tego zadania było pewien fakt z geometrii sfery (czyli moim celem jako autora zadania było wymyślenie zadania, które dałoby się łatwo rozwiązać znając ten fakt). Wyobraźmy sobie, że Ziemia ma promień 1, i rysujemy na niej trójkąt sferyczny, którego dwa wierzchołki leżą na równiku w odległości 90 stopni od siebie, a trzeci jest na biegunie. Każdy kąt tego trójkąta ma 90 stopni, czyli suma jest 270 stopni - o 90 stopni, czyli π/2, za dużo. Dla małych trójkątów suma kątów jest bliska 180 stopni; nasz trójkąt jest bardzo duży, jego pole to 1/8 powierzchni sfery, czyli π/2. Możemy też wziąć dopełnienie naszego trójkąta; to też jest trójkąt sferyczny, którego każdy kąt ma 270 stopni, czyli jego suma kątów, 810 stopni, to o 630 stopni = 3,5π za dużo; pole tego trójkąta to 7/8 powierzchni sfery, czyli 3,5π.
Podobne zadanieOryginalnie zadanie zgłosiłem w 2 wariantach. W drugim wariancie struktura piłki była inna: na każdej ścianie dwunastościanu foremnego połączono punkt środkowy z każdym jego wierzchołkiem, otrzymając bryłę o 72 wierzchołkach, której ściany to 60 trójkątów. Tą wersję zadania chyba trudniej zrobić przez rozrysowanie, budowę, albo ze wzoru Eulera; jednak bardzo łatwo jest je zrobić korzystając ze wzoru z geometrii sfery (tym razem pole trójkąta jest znane — 1/60 powierzchni sfery, jak również miary wszystkich kątów - 1/5 albo 1/6 kąta pełnego, zatem nie musimy rozwiązywać żadnego układu równań ani traktować nieznanych wartości w sposób symboliczny). (4 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com