Niektórych rzeczy po prostu nie da się zrobić. Prawda stara jak świat, a jednak ciągle potrafi zaskakiwać. W artykule opowiemy o spacerze, który nie mógł się udać i o dwóch podobnych problemach, które z tego wynikają.
Wrocław nazywany jest "miastem stu mostów". Odra wyraźnie nie potrafi zdecydować się jak chce przepłynąć przez miasto. Więc przepływa trochę tu, trochę tam, rozgałęzia się i zlewa z powrotem. A wrocławianie budują mosty. Ci z Czytelników, którzy tu mieszkają, pewnie kojarzą okolice Wyspy Słodowej. Z lotu ptaka wygląda to mniej więcej tak.
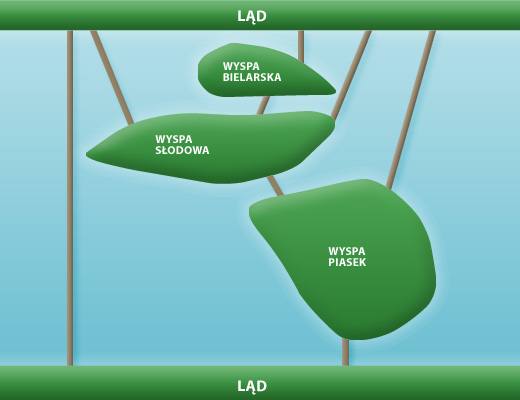
Spacerując kiedyś po okolicy, postawiłem sobie zadanie. Zaczynając z północnego brzegu Odry, chciałem przejść przez każdy z zaznaczonych na rysunku mostów dokładnie raz, wracając ostatecznie do punktu startu. Pierwsza próba przyniosła niepowodzenie - przeszedłem wprawdzie przez wszystkie osiem mostów, ale spacer skończyłem na Wyspie Piasek. Następnych prób już nie było. Czy domyślasz się, dlaczego?
Stojąc na Wyspie Piasek popatrzyłem na pierwszy z jej mostów. Później na drugi. Wreszcie na trzeci. No właśnie. Na Wyspę prowadzą trzy mosty. Jeśli każdy z nich chciałbym przejść dokładnie raz, nieuchronnie utknę na wyspie! Skoro zaczynam poza nią, to po przejściu pierwszego z jej mostów będę na wyspie, po przejściu drugiego poza wyspą, po przejściu trzeciego znowu na wyspie.. i nie będzie już wolnego mostu, którym mógłbym ją opuścić! W takim razie problemu, który sobie postawiłem, nie dało się nijak rozwiązać. To trochę pomogło pogodzić się z porażką.
Po jakimś czasie dowiedziałem się, że prawie 300 lat temu nad bardzo podobnym problemem zastanawiał się słynny szwajcarski matematyk Leonard Euler. W jego przypadku chodziło o podobny spacer po mostach i wyspach - tyle, że nie Wrocławia, a Królewca. Zagadnienie okazało się potem bardzo zasłużone dla matematyki, bo dało początek temu, co teraz nazywamy teorią g.. . Znasz już, Czytelniku, pojęcie grafu? Mówiąc najkrócej, graf to pewna liczba wierzchołków (punktów) połączonych krawędziami (odcinkami). Nie ma znaczenia ich ułożenie na płaszczyźnie (grafy nie mają nic wspólnego z geometrią!), liczy się tylko to, które wierzchołki są połączone. Grafy pozwalają wygodnie patrzeć na przeróżne interesujące problemy. Spójrz:
 | 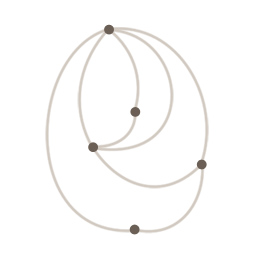 |
Nasz problem spaceru po Wrocławiu, to typowy problem grafowy. Jego graf składa się z wierzchołków (kawałków lądu we Wrocławiu) i łączących je krawędzi (mostów). Zadanie można teraz opowiedzieć inaczej - narysuj zadany graf na kartce nie odrywając ołówka od papieru, rysując każdą krawędź tylko raz i kończąc rysowanie w wierzchołku od którego zacząłeś. Pewnie widziałeś podobne zagadki w kolorowych czasopismach. Po trzech akapitach poświęconych tej specjalnej drodze w grafie czas już nadać jej jakąś nazwę; matematycy umówili się nazywać ją na pamiątkę wspomnianego uczonego cyklem Eulera.
- Cykl Eulera - droga w grafie, która przechodzi przez każdą krawędź dokładnie raz i kończy się w wierzchołku, w którym się zaczęła.
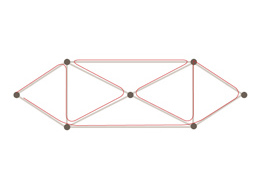
Na przykładzie problemu mostów wrocławskich zauważyliśmy, że aby w grafie istniał cykl Eulera, wszystkie jego wierzchołki muszą mieć parzysty stopień (stopień wierzchołka to po prostu liczba "przymocowanych" do niego krawędzi); ponieważ po każdym wejściu do wierzchołka, musimy z niego wyjść. To pozwala nam łatwo powiedzieć o niektórych grafach, że na pewno nie mają cyklu Eulera. Nie wiemy natomiast czy jest to warunek "wystarczający", czyli, czy każdy graf z parzystymi stopniami wierzchołków faktycznie ma cykl Eulera.
W rzeczywistości każdy graf, którego wierzchołki mają parzyste stopnie ma cykl Eulera, chociaż na razie będziemy musieli uwierzyć w to na słowo honoru. Podsumujmy:
- W grafie istnieje cykl Eulera wtedy i tylko wtedy, kiedy wszystkie jego wierzchołki mają stopień parzysty (oczywiście, pod warunkiem, że jest "spójny", to znaczy z każdego wierzchołka da dojść do dowolnego innego)
I na tym na razie skończymy temat cyklu Eulera. Nie wyjaśniliśmy sobie wszystkiego, bez odpowiedzi pozostawiamy na przykład pytanie "W jaki sposób znajdować cykl Eulera, kiedy już wiemy, że istnieje?". Udzieleniu odpowiedzi na te i kilka innych pytań poświęcimy jeden z kolejnych artykułów. A póki co, czas przedstawić drugiego bohatera niniejszego tekstu - problem cyklu Hamiltona.
- Cykl Hamiltona - droga w grafie, która przechodzi przez każdy wierzchołek dokładnie raz i kończy się w wierzchołku, w którym się zaczęła.
(nazwa upamiętnia rzecz jasna Williama Hamiltona, irlandzkiego matematyka, nie sportowca o tym samym nazwisku)
Trochę zmodyfikowaliśmy wcześniejszy problem. Zmiana nie jest duża - teraz będziemy szukać cyklu, który niekoniecznie przechodzi przez wszystkie krawędzie. Wszystko, czego będziemy od niego oczekiwać, to odwiedzenie dokładnie raz każdego z wierzchołków. Na przykład tak:
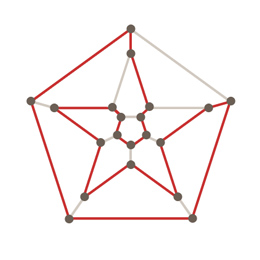
W matematyce często podobne problemy mają podobne rozwiązania. Warto zastanowić się, czy można, rozumując podobnie jak przy cyklu Eulera, określić które grafy posiadają cykl Hamiltona. Kilka pokoleń matematyków próbowało to zrobić, bezskutecznie. Lata mijają, a problem wciąż czeka na swojego zdobywcę (czeka, dodajmy, z pieniędzmi i sławą). Póki co potrafimy wskazać kilka grafów, które mają cykl Hamiltona i kilka, które na pewno go nie mają, ale na tym nasza wiedza się kończy. Ciągle jedyną pewną metodą na rozstrzygnięcie istnienia takiego cyklu w danym, dowolnym grafie, pozostaje mozolne sprawdzanie wszystkich istniejących ścieżek. Dla grafów o kilkudziesięciu wierzchołkach zadanie staje się zbyt czasochłonne nawet dla najlepszych współczesnych superkomputerów.
A lepsze rozwiązanie przydałoby się bardzo - nie tylko matematykom! Problem cyklu Hamiltona występuje pod różnymi postaciami w przeróżnych dziedzinach aktywności człowieka. Turysta podróżujący komunikacją miejską, który chce odwiedzić kilka miejsc w mieście - ale żadne dwa razy - rozwiązuje.. właśnie problem cyklu Hamiltona! A co z przemysłem? Ciężka maszyna do prowadzenia odwiertów dla przemysłu naftowego może być przewożona tylko po istniejących, szerokich drogach asfaltowych. Czy da się odwiedzić każde z miejsc do zbadania tak, aby przez żadne nie przejeżdżać dwa razy? Znowu Hamilton! I znowu współczesna informatyka jest - póki co - bezradna.
Problemy, które dzisiaj poznaliśmy, sformułowane są podobnie. Różnica okazuje się jednak wystarczająco znacząca, aby cykle Eulera i Hamiltona znalazły się po przeciwnych stronach granicy współczesnej wiedzy - o pierwszym z nich wiadomo już wszystko, o drugim wciąż niewiele. Jest więc pole do popisu, ale badania nad teorią grafów warto zacząć od prostszych ćwiczeń, których kilka podaję poniżej.
Kilka nietrudnych zadań.
1. Znajdź cykl Eulera w grafie.
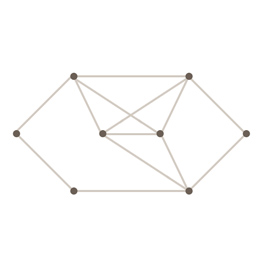
2. Ile minimalnie mostów trzeba dobudować we Wrocławiu, żeby wyjściowy problem spaceru dało się rozwiązać?
3. A co jeśli zamiast cyklu Eulera będziemy szukać "ścieżki" Eulera - czyli drogi, która przejdzie każdą krawędź grafu dokładnie raz, ale niekoniecznie musi wrócić do wierzchołka w którym się zaczęła? Które grafy mają ścieżkę Eulera?
Co dalej?
Czytelnikom nieco już wprawionym w teoriografowej terminologii polecam świetne, kompleksowe omówienie tego, co o problemie cyklu hamiltona już wiadomo: http://www-users.mat.uni.torun.pl/~kbunka/cykleham.pdf .
Zaawansowanych czytelników zapewne zainteresuje krótka, ale treściwa praca poświęcona kolejnemu pokrewnemu problemowi - cyklowi komiwojażera. http://www.mimuw.edu.pl/delta/artykuly/konkurs_prac_uczniowskich/4problem.pdf .
Ja tymczasem dziękuję za lekturę, i do następnego razu!
Rysunki: Natalia Fleszar











